HAMILTONIAN OF CEF AND MAGNETIC INTERACTIONS
The coulomb potential V at a point with coordinates (r, θ, φ) spaced from the beginning of the coordinate system by vector r, is directly proportional to the sum of charges spaced from the beginning of the coordinate system by vectors Ri and inversely proportional to the distance between them and that point:
![]()
where the summation expands to all external point charges, or has a spherical-symmetric expansion. By defining α as the angle between R and r, we can represent the quotient on the right side of the above equation as the sum of the Legendre function:
![]()
This expression is true for r < R. There is a simple connection between the Legendre functions and spherical harmonics:
![]()
As a result, the potential V(r, θ, φ) of charges qi can be represented as follows:
![]()
Similarly, based on the so-called tesseral harmonics defined as follows:
![]()
Potential V can be represented as:
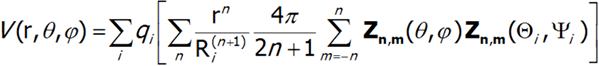
For further considerations it is convenient to assume knowledge of the distribution of qi charges and replace all values that describe it with a single set of parameters Amn:
![]()
Taking into account that although the coefficients Amn may be grouped in the overall situation, the conditions for reality and hermiticity of potential V require that:
![]()
Potential V can therefore be represented in the general form:
![]()
Only a few expressions in the above multipole series are non-zero in nature. The non-vanishing matrix elements of the V potential between single-electron states |l, lz> and |l, l’z> can only be those that simultaneously meet two conditions:
1. n ≤ 2l (triangle condition for integrals of spherical harmonics) 2. l’- l ± m = 0
The triangle condition suggests that in the case of d electrons, the value n ≤ 4, while for f electrons, the value n ≤ 6. These conditions allow specifying the number of nonzero coefficients describing the electrostatic potential. When considering the electrons d or f, the Amn coefficients may be grouped, although the conditions for reality and hermiticity of potential V can only be up to 27:
![]() .The existence of a center of symmetry in the central ion's environment implies a reduction of coefficients with odd n value; this is the so-called parity condition. Consideration of the environmental symmetry leads to the conclusion that the presence of the axis of symmetry reduces the number of nonzero coefficients Amn. In the case of 2-, 3-, 4- and 6-fold axes, that number is 15, 9, 7 and 5, respectively. Knowing the symmetry of the environment of the paramagnetic ion, based on knowledge of tesseral harmonics, we can calculate individual expressions of the multipole V potential in Cartesian coordinates. The single-electron Hamiltonian of the crystal field interaction can therefore be generally represented as a multipole expansion:
.The existence of a center of symmetry in the central ion's environment implies a reduction of coefficients with odd n value; this is the so-called parity condition. Consideration of the environmental symmetry leads to the conclusion that the presence of the axis of symmetry reduces the number of nonzero coefficients Amn. In the case of 2-, 3-, 4- and 6-fold axes, that number is 15, 9, 7 and 5, respectively. Knowing the symmetry of the environment of the paramagnetic ion, based on knowledge of tesseral harmonics, we can calculate individual expressions of the multipole V potential in Cartesian coordinates. The single-electron Hamiltonian of the crystal field interaction can therefore be generally represented as a multipole expansion:
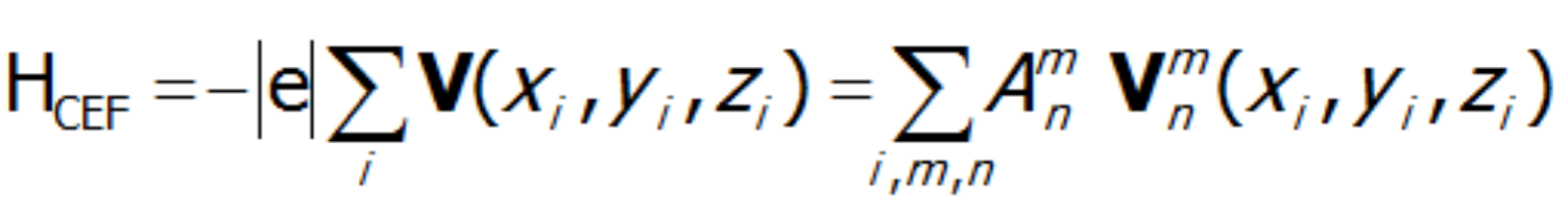
where i numbers the electrons of the unclosed shell and the basic components of the expansion of potential V(x,y,z) take the known form:
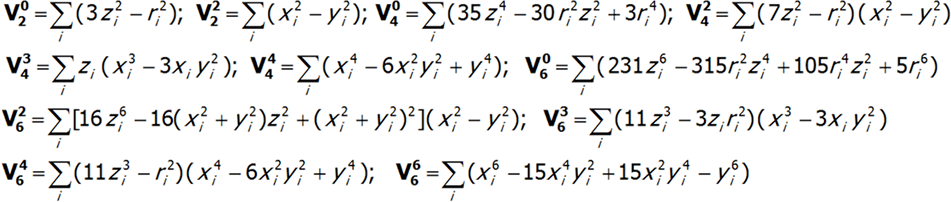
The shape of multipole components Vmn of potential V in Cartesian coordinates is presented in Fig.2.4-7. Multipole potentials Vmn in Cartesian coordinates are homogeneous polynomials of the n degree; in view of the commutation relations of operators Lx, Ly and Lz, we may therefore construct expressions that transform in the same way as them, based on operators J+, J_ and Jz. It should be remembered that: L+= Lx + iLy i L_= Lx - iLy and that: {L+, L_}=2Lz, {Lz, L+}= L+, {Lz, L_}= - L_.
The equivalent form of the Hamiltonian, constructed based on Stevens operators: ![]() , is different from the potential form by a proportionality factor θn and by the mean value of the power of n of the radius of the unclosed shell d or f. In view of the fact that describing the components of the potential requires using the operators of the components of the electron shell's total angular momentum, the eigenstates of this Hamiltionian are multi-electron states. A multi-electron Hamiltonian of an ion in the unclosed f shell in a |J, JZ> space will take the following form:
, is different from the potential form by a proportionality factor θn and by the mean value of the power of n of the radius of the unclosed shell d or f. In view of the fact that describing the components of the potential requires using the operators of the components of the electron shell's total angular momentum, the eigenstates of this Hamiltionian are multi-electron states. A multi-electron Hamiltonian of an ion in the unclosed f shell in a |J, JZ> space will take the following form:![]() .
.
The strictly defined CEF Hamiltonian, complete with a spin-orbit coupling, realized in the full |L,S,Lz,Sz> space will take the form:
![]()
.
For the record, the full Hamiltonian, realized by ATOMIC MATTERS MFA, complete with full magnetic interactions is as follows:
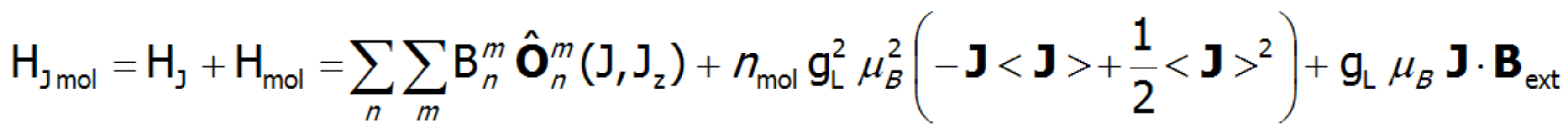
According to the adopted notation, the multiplicative scale factors θn for n = 2, 4 and 6 are marked by the first Greek letters, i.e.: θ2 = α, θ4 = β, θ6 = γ. The method for calculating the potential-scaling factors in the language of equivalent operators for states with the same J was presented by K.W.H. Stevens. The values of factors α, β and γ for all ion multiplets can be calculated by the ATOMIC MATTERS software. The major Stevens operators in the original notation are as follows:
Knowing the matrix elements of operators Jz, J+, J_ in the |J,Jz> space:
![]()
we can construct a matrix for the simplified Hamiltonian for the |J,Jz> space. While knowing the matrix elements of the operators Lz, Sz, Lx and Sx , as well as the matrix elements of the spin-orbit coupling, which are not only diagonal elements:
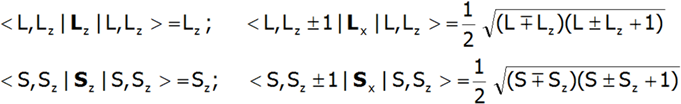
We will construct the full Hamiltonian CEF for the |L,S Lz,Sz> space; complete with Mean Field Approximation of magnetic ion-ion interactions, it is as follows:
![]()
It is possible to calculate the Amn coefficients based on the values of the distance between the coordinating ligands and the magnetic ion by using the so-called point-charge model. It turns out that, despite the simplification (ligands treated as charged balls with a homogeneous surface charge distribution, lack of effects screening the shell 4f by shells 5s and 5p) the point-charge model for ionic bonds generates the structure of states close to that observed experimentally.
The point-charge model is too simplistic in the case of intermetallic bonds. On the other hand, the shell 4f in intermetallic bonds retains its integrity and the crystal lattice environment of the paramagnetic ion usually has a well-defined symmetry. Hence, the above reasoning, which only imposes conditions for the symmetry of the shell's environment, remains true, even though we can no longer apply the direct method for determining Amn the parameters, based exclusively on knowledge of the distances between coordinating ions. In such situations, it is convenient to treat the product of values characterizing the contribution of individual multipoles (i.e.:) as a parameter of the crystal field Bmn . The Hamiltonian parameterized in such a way is as follows:
![]()
of course, the number of non-zero Stevens elements in the Hamiltonian CEF depends on the symmetry of the environment of the paramagnetic ion in the crystal structure. In the case of a field with diamond-shaped symmetry, part of the Hamiltonian associated with the impacts by the CEF Hamiltonian electric field contains the following expressions:
![]()
for the environment with a hexagonal structure:
![]()
for the tetragonal environment, Hamiltonian CEF is as follows:
![]()
While the cubic field is described by the following Hamiltonian:
![]()
In view of the relationship between the parameters of cubic crystal field, the Hamiltonian of cubic fields (coordination with a tetrahedron, octahedron or cube) only has two independent parameters, which are often as follows:
![]()
The structure of states in a cubic field is sometimes represented in its simplified form on so-called LLW diagrams after parameterizing the parameters to B4 and B6. This parameterization is based on entering two new values x and W. The purpose of this procedure is based on the fact that factor x is the true variable determining the system of levels, and factor W merely scales the energy. The relationships between parameters B4 and B6 as well as x and W are as follows:
![]()
F(4) and F(6) are fixed values for a given element and depend on the total angular momentum J of the basic multiplet.
a)
b)
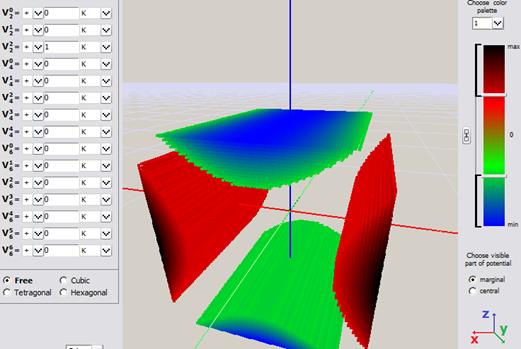
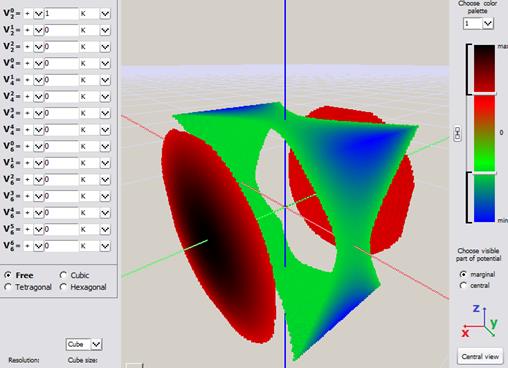
Fig.Fig. Simple visualization from an early version of ATOMIC MATTERS CEF VISUALIZER showing the potential of electrostatic multipoles acting on the paramagnetic ion in Cartesian coordinates:
a) Potential of quadrupole V02 b) Potential of quadrupole V22
The factors of the CEF crystal field are Anm coefficients. They characterize the charge distribution in the environment of an atom/ion by determining the components of expansion of the multipole external potential of an ion/atom. Other parameters that can be used to determine the crystal field are the so-called Bnm parameters. For these parameters, the Hamiltonian can no longer be created based on the potential V, but on Stevens operators and their parameterization. In summary, the ATOMIC MATTERS application performs calculations based on: the local symmetry of the paramagnetic ion environment, electrostatic field of coordinating ligands (CEF) and the spin-orbit interaction (so) inside ions. On the other hand, using the properties of the equivalent operator method (Wigner-Eckart theorem) multipole components of potential V, the equivalent Hamiltonian HCEF is written in a concise form:
![]()
which provides the visualization of the CEF potential, together with a set of calculation results in the CEF Potential output tab and, in the main application window, in the POTENTIAL VISUALIZER tab.
BIBLIOGRAPHY
- Margenau & G.M. Murphy, The mathematics of Physics and Chemistry, Princeton, New Jersey (1956).
- Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 215 (1953) 437.
- Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 218 (1953) 553.
- M.T. Hutchings, Solid State Phys. 16 (New York 1964 ) 227.
- Fulde in: Handbook on the Physics and Chemistry Rare Earth, Vol. 2 North-Holland. Inc. (1979).

