INTRODUCTION
ATOMIC MATTERS can simulate the basic solid compound properties of transition metals and rare earth metals. Our approach is based on Crystal Field Theory. A Crystal Electric Field with the recognizable 'CEF' abbreviation (some scientists use other abbreviations, e.g. CF - Crystal Field, ZFS - Zero Field Splitting) combined with strict modern computational methods, which makes it possible to predict the magnetic and electronic properties of chemical compounds in a solid state. This theoretical approach is deeply rooted in atomic physics and is based on the methods first defined by H.A. Bethe in 1929 (Ann. Phys. Lpz. 3 (1929) 133) and developed by the great scientists: J.H.van Vleck, B.G. Wybourne, A.Abragam, B.Blaney, E.U. Condon, G.H. Shortley, R.J. Elliot, K.W.H. Stevens, G. Racah, B.R. Judd, P.G de Gennes, J.Mulak, R.J.Radwański, C. Rudowicz, D.J.Newman, and many others. These calculation methods have been elaborated over decades and are now implemented in ATOMIC MATTERS.
CRYSTAL ELECTRIC FIELD (CEF)
The theory based on the crystal field idea was first proposed by H.A. Bethe in 1929; this approach indicated the possibility of predicting how the degeneration of paramagnetic ions multiplets can be prevented by interactions coordinated by ligands. The basic idea of this theory was that, in accordance with the well-known (for 16 years at the time) Stark phenomenon, the electric field of coordinating ions must affect the electron states of paramagnetic ions, causing them to split depending on the angular momentum values of quantum numbers. Calculations based on group theory suggested that quantitative prediction of the method for splitting electron states was possible, depending on the point group symmetry of the crystal lattice environment of the magnetic ion. The following theses lie at the core of crystal field theory (CEF - Crystal Electric Field):
- The forces responsible for the occurrence of a coordination bond and its stability are electrostatic in nature.
- Regardless of their actual structure, ligands are treated as a source of electrostatic charge. The spatial arrangement of these charges determines the symmetry of the electrostatic field affecting the central ion.
- The electron configuration of the central ion is determined based on quantum-mechanical rules that are typical of atomic physics and the fine-structure of terms and multiplets.
CEF theory is based on operator equivalent techniques (which are in turn are based on the Wigner-Eckart theorem), which is a relatively simple method to quantify the value of state fission with the same value of total angular momentum J in an unclosed electron shell in the crystal field. The basic idea behind the operator equivalent technique is to expand the electrostatic potential of ligands into a multipole series. One then seeks such angular momentum operators that are the combinations J+, J_ and Jz, which meet the same transformational relationships as the corresponding components of the potential expansion into the multipole series (it is necessary that J is a good quantum number). Where J is not a good quantum number, as is the case when calculating the influence of the crystal field CEF on d-electron configurations, the construction of equivalent operators is analogous and based on L+, L_ and Lz.
FINE ELECTRONIC STRUCTURE
Fine electronic structure, related to atomic-like states and determined by the crystal-field and spin-orbit interactions, has been evaluated by means of different experimental techniques. The importance of the higher-order charge multipolar interactions and the local symmetry of the crystal field for the realized fine electronic structure and for the ground state are emphasized: the significant successes of crystal-field theory indicate the substantial preservation of the atomic-like structure of open-shell atoms even when they become part of a solid. Extending CEF theory to a quantum atomistic solid-state theory is proposed.
A discrete electronic structure contains a number of states grouped in terms and multiplets. It is related to the incomplete 2p, 3p, 3d, 4d, 5d, 4f or 5f shell. The inner 3d shells are closed, thereby forming the core 18Ar. The inner 4f shells are closed and form the 54Xe core. Terms, a subset of states characterized by the same values of total L and S quantum numbers, are formed by non-central Coulomb interactions. States of terms are grouped in multiplets, characterized by the same L, S and J, and are formed by spin-orbit interactions that are much stronger for rare-earth ions than CEF interactions. The strong spin-orbit coupling makes J become a relatively good quantum number, because the first excited multiplet is at least ~130 meV (1500 K) above the primary multiplet. If the temperature rises in thermally polluted states, higher states are occupied according Boltzmann’s law. In this case, a 2J+1-fold degenerated primary multiplet split by an external CEF field can be treated as the basic contribution to the analysis of such systems' properties. Hund principles are applied to determine the primary multiplet in the case of approximate calculations for basis |J,Jz>:
- The ground state of the terms' structure has the maximum value S allowed by the Pauli exclusion principle.
- The ground state has a maximum allowed L value, with maximum S.
- The primary multiplet has a corresponding J=|L-S| when the shell is less than half full, and J=L+S when more than half full.
The S, L and J of the ground multiplet are determined by Hund’s rules. The ground multiplet is 2J+1 degenerated as its degeneracy is removed by CEF interactions and magnetic interactions. CEF interactions and magnetic interactions somehow resemble the Stark and Zeeman effect known from atomic physics. The energies and eigenfunctions of the discrete fine electronic structure are obtained by diagonalization of the (2J+1)-dimensional matrix. The fine electronic structure can be directly detected by many different spectroscopic methods, one of the best of which is Inelastic Neutron Scattering (INS) experiments.
For the full computations necessary for a strong CEF (3d ions), the fine structure levels are grouped into systems T2g, Eg, A2g, showing no affiliation to specific multiplets. In such cases, it is necessary to take into account the whole structure of terms through diagonalization of the Hamiltonian with the matrix of (2L+1)(2S+1).
Strong cubic CEF (for 3d ions) interactions form groups of levels (e.g. T2g, Eg, A2g) which are partially split by spin-orbit interactions and, if they occur, lower symmetry CEF interactions. The energies and eigenfunctions of the discrete fine electronic structure (for the lowest term) are obtained by diagonalization of the (2L+1)(2S+1)-dimensional matrix. In the temperature T = 0[K] (absolute zero), only the lowest state is occupied. The magnetic moment at T=0[K] is equal to the moment of the ground state. This makes it possible to evaluate the total, spin and orbital moments. The eigenstates and corresponding eigenfunctions, |Γn>, can be found from direct diagonalization of the Hamiltonian CEF. The CEF levels are denoted by the irreducible representation |Γn>, and the corresponding wave functions (according chosen calculations base) are: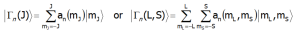
SPECTROSCOPIC OBSERVABILITY OF INTERSTATE TRANSITIONS
Fine electron structure is observed in a number of spectroscopic methods (EPR ESR, IR spectroscopy, Raman scattering, etc.). Currently, the best method of exploring the fine electron structure is Inelastic Neutron Scattering (INS). For a system of N identical ions, a differential cross section in the INS experiments is assumed as follows:
![]() In the above equation γN is the gyromagnetic factor of the neutron, re is the classical radius of the e electron re=e2/(mec2)=2.818·10-15m, ki and kf are the wave vector of the incident and reflected neutron, respectively, and the expression exp(-2W(ki-kf)) represents the Debye-Waller factor, which describes the thermal excitation of vibrations in atoms. The delta functionδ (ω - Ej+Ek) corresponds to infinitely narrow crystal field states and is often replaced in exact calculation with the Lorentz distribution with specified half widths at half maximum (FWHM) of CEF states. The square of matrix elements from the above equation, symbolically denoted as <Γk|J┴|Γj>2 in the case of a polycrystalline material for dipole transitions is replaced with
In the above equation γN is the gyromagnetic factor of the neutron, re is the classical radius of the e electron re=e2/(mec2)=2.818·10-15m, ki and kf are the wave vector of the incident and reflected neutron, respectively, and the expression exp(-2W(ki-kf)) represents the Debye-Waller factor, which describes the thermal excitation of vibrations in atoms. The delta functionδ (ω - Ej+Ek) corresponds to infinitely narrow crystal field states and is often replaced in exact calculation with the Lorentz distribution with specified half widths at half maximum (FWHM) of CEF states. The square of matrix elements from the above equation, symbolically denoted as <Γk|J┴|Γj>2 in the case of a polycrystalline material for dipole transitions is replaced with ![]() In the case of a single crystal, the intensity of neutron scattering for dipole transitions between CEF states (Γj and Γk) is represented by the following equation:
In the case of a single crystal, the intensity of neutron scattering for dipole transitions between CEF states (Γj and Γk) is represented by the following equation: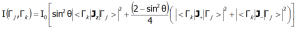 where θ is the angle between the neutron beam and the quantization axis z. INS is a very powerful tool for experimental verification of the theoretically calculated fine structure of electron states. Note, however, that not all CEF states are visible using this technique - only the transitions between states, where: |<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| is non-zero. ATOMIC MATTERS can calculate the Fine Electronic Structure of ions/atoms in user's choise -dependent spaces, conventions and unit systems together with matrix elements: |<Γk|Jz|Γj>|, |<Γk|J-|Γj>| and |<Γk|J+|Γj >| or analogic: |<Γk|Lz|Γj>|, |<Γk||<Γk|Sz|Γj>|, |<Γk|L-|Γj>|, |<Γk|L+|Γj >|, |<Γk|S+|Γj >| and |<Γk|S-|Γj>| for integrated ATOMIC MATTERS Spectra Simulations.
where θ is the angle between the neutron beam and the quantization axis z. INS is a very powerful tool for experimental verification of the theoretically calculated fine structure of electron states. Note, however, that not all CEF states are visible using this technique - only the transitions between states, where: |<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| is non-zero. ATOMIC MATTERS can calculate the Fine Electronic Structure of ions/atoms in user's choise -dependent spaces, conventions and unit systems together with matrix elements: |<Γk|Jz|Γj>|, |<Γk|J-|Γj>| and |<Γk|J+|Γj >| or analogic: |<Γk|Lz|Γj>|, |<Γk||<Γk|Sz|Γj>|, |<Γk|L-|Γj>|, |<Γk|L+|Γj >|, |<Γk|S+|Γj >| and |<Γk|S-|Γj>| for integrated ATOMIC MATTERS Spectra Simulations.
BIBLIOGRAPHY
- R.J. Radwanski, N.H. Kim-Ngan, F.E. Kayzel, J.J.M Franse, D. Gignoux, D. Schmitt, F.Y. Zhang, J. Phys.: Condens. Matter 4 (1992) 8853.
- R.J. Radwański, Z. Ropka & R. Michalski in: Magnetism and Electronic Correlations in Local-Moment Systems: Rare Elements and Compounds, edited by M. Donath, P.A. Dowben & W. Nolting, World Scientific (1998) 445-453
- H. Margenau & G.M. Murphy, The matematics of Physics and Chemistry, Princeton, New Jersey (1956).
- J. Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 215 (1953) 437.
- J. Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 218 (1953) 553.
- M.T. Hutchings, Solid State Phys. 16 (New York 1964 ) 227.
- P. Fulde in: Handbook on the Physics and Chemistry Rare Earth, Vol. 2 North-Holland. Inc. (1979).
- C. Rudowicz, J. Phys. C: Solid State Phys. 20 (1987) 6033.
- K. Huang Podstawy fizyki statystycznej PWN 2006; Tłumaczenie: Magdalena Załuska-Kotur
- P.W. Atkins Chemia Przewodnik po chemii fizycznej PWN 1997

