THERMODYNAMICS OF MULTI-ELECTRON SYSTEMS
The presented approach carries enormous analytical potential. The calculated states and eigenenergies of the presented Hamiltonian allow the prediction of a number of electron and magnetic properties of compounds. The structure of states obtained by solving the Hamiltonian eigenequation makes it possible to calculate a compound’s magnetic properties at extremely low temperatures, including the value of the magnetic moment of an ordered state, its direction, and the behavior of magnetic moments after the application of an external magnetic field. It is also possible to calculate changes in the system's physical properties with increasing temperature, when the values (and possibly directions) of magnetic moments change, similar to the change of the splitting of fine structure states in a self-aligned molecular field. The presented approach facilitates analysis of the mechanism of the formation of magnetic moments and the formation of the magnetic order.
At a temperature of T = 0 K, only the ground state is occupied. In this situation, the magnetic moment of the ion is exactly equal to the momentum of the ground state. At extremely low temperatures, it is possible excite the system, for example by magnetic interaction with low-energy neutrons (as is used in Inelastic Neutron Scattering Spectroscopy, INS). However, it should be remembered that the observed transitions are excitations from the ground state. When the temperature rises, the probability of occupying higher states increases according to Boltzmann statistics. The number of ions with energy Ei within a system with a temperature T, is: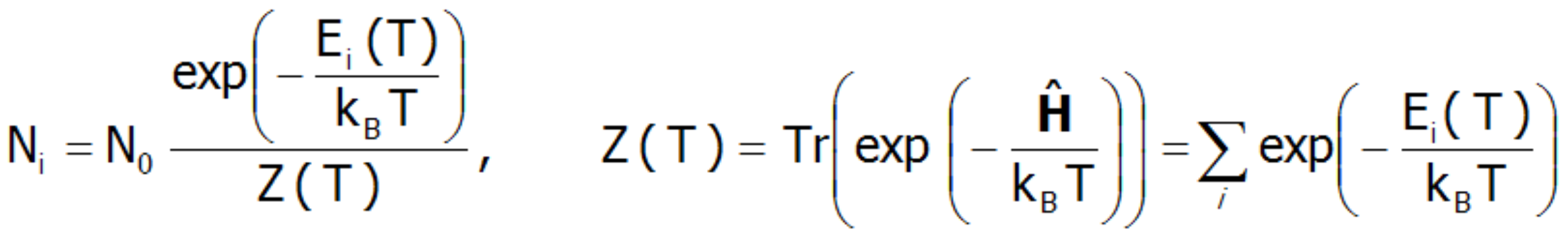
In the above expression, N0 denotes the total number of particles, and Z(T) is a statistical sum of states (separation function). Knowing the statistical sum of the states, we can determine the Helmholtz free energy F(T):
![]()
Therefore, the internal energy of the U(T) system can be estimated: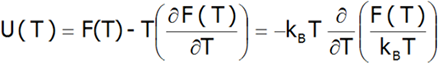
where:
kB= 1,38 x 10 -23 J/K (Boltzmann constant)
Based on knowledge of thermodynamic state functions [7], we can specify a number of properties defined based on them. In particular, Helmholtz thermal dependence of free energy F(T) allows for the analysis of the thermal evolution of the properties of d or f-electron systems. A discussion of the various properties of the compounds calculated based on the presented method at T ≠ 0 is shown below. The fine structure of states (Ei, Γi) makes it possible to determine the thermodynamic functions for the statistical group of N ions. The most sensible value is N=N0≈6.022.1023 mol-1 (Avogadro constant).
ENTROPY
Calculating the entropy of the localized electron system in an unclosed shell d or f is reduced to calculation of the integral:
![]()
where c(T) is the system's calculated molar specific heat taken as a derivative of the total internal energy: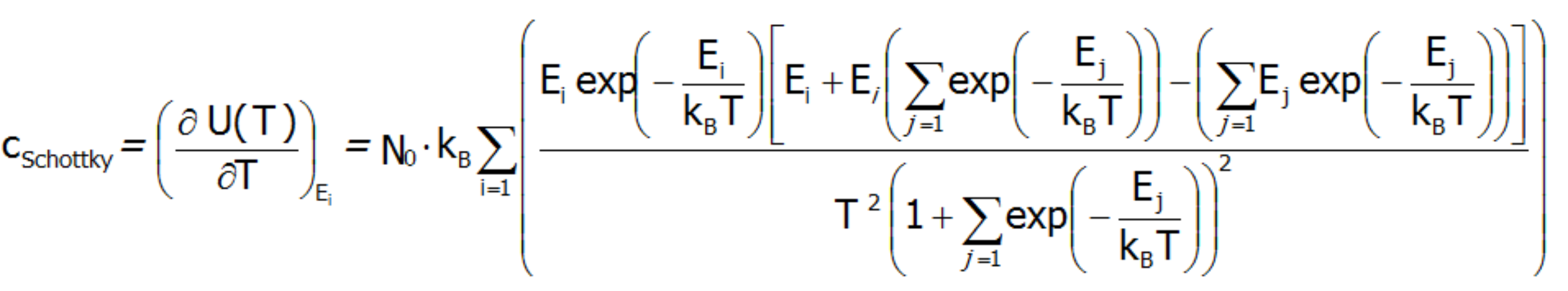
or directly as a second derivative of the Helmholtz free energy: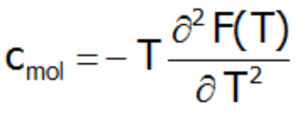
and S is also defined as:![]()
which in conjunction with the definition of statistical entropy allows the number of occupied states of the fine electron structure at a specific temperature to be specified.
MAGNETIC MOMENT AND MAGNETIZATION
In the applied methodology, calculating the magnetization boils down to summing the identically behaving magnetic moments of individual ions with an unclosed electron shell. Due to the fact that transition metal ions are in the self-aligned molecular field, their magnetic moment value changes with temperature. Bearing in mind that each eigenstate of the CEF Hamiltonian is related to its magnetic moment, the total moment of a strongly correlated electron system at a given temperature is the resultant moment of occupied states calculated with the inclusion of the Boltzmann weight: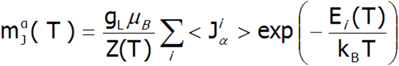
In the above equation, the α index is a directional component, i - numbers the Hamiltonian eigenstates, while <Jiα> represents the expected value of the total angular momentum on the α axis in the i-th state. It should be emphasized that at T = 0, when only the ground state is occupied, the magnetization of the ion system 4f per 1 ion is equal to the expected value of the magnetic moment of the ground state. Due to the fact that all ions behave identically in this model, the calculated temperature dependence of the magnetic moment is closely linked to the value of the molecular field, which is:![]()
The value of the molecular field factor nmol determines the temperature at which the magnetic order Tc occurs. Calculations of magnetization in the ordered state can determine the magnetocrystalline anisotropy of the system. In the case of tetragonal symmetry, the expansion of the anisotropy energy can be represented in a known form:![]()
where Ki(T) are coefficients of anisotropy dependent on the temperature, and θ and φ are polar angles describing the direction of the magnetic moment relative to the perpendicular crystallographic axes. The coefficients Ki(T) are closely related to the parameters of the crystal field. In a field with tetragonal symmetry they have the following value: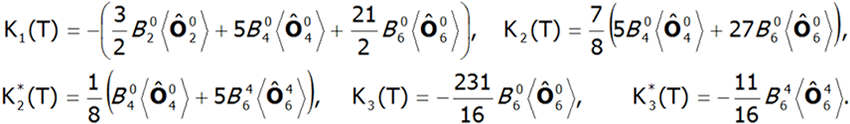
where:![]() -represents the average temperature of Stevens operators. The direct determination of magnetocrystalline anisotropy is possible by calculating the value of induced magnetic moments in an external field applied in different directions. With this approach, the components of the total magnetic moment of paramagnetic ions can be clearly determined. The total magnetic moment of the ion consists of the orbital and spin sections: mc=mL+mS. Knowledge of the expected values of the momentum vector components of each state <Jiα> makes it possible to specify the share of the spin and orbital sections of the magnetic moment. Bearing in mind that: Jz=Lz+Sz and taking into account that gl = 1 and gs = 2.002324:
-represents the average temperature of Stevens operators. The direct determination of magnetocrystalline anisotropy is possible by calculating the value of induced magnetic moments in an external field applied in different directions. With this approach, the components of the total magnetic moment of paramagnetic ions can be clearly determined. The total magnetic moment of the ion consists of the orbital and spin sections: mc=mL+mS. Knowledge of the expected values of the momentum vector components of each state <Jiα> makes it possible to specify the share of the spin and orbital sections of the magnetic moment. Bearing in mind that: Jz=Lz+Sz and taking into account that gl = 1 and gs = 2.002324:
![]()
we will have reached:
![]()
The above relationships indicate that the ratios of each component of the magnetic moment to the total momentum are fixed for a given ion and independent of their environment and temperature: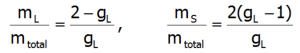
The issue of the accuracy of the above reasoning is discussed at the beginning of the description of the theoretical bases of application, while comparing the results of calculations performed on the basis |J,Jz> in relation to the calculations carried out for the fuller basis |L,S,Lz,Sz> taking into account the coupling between the states of different multiplets. Determining the value of the orbital and spin components of the magnetic moment of the paramagnetic ion with an electron structure calculated in the representation |L,Lz,S,Sz> boils down to a simple interpretation of the expected values L and S.
An external magnetic field eliminates the degeneracy, changes the energy value of the states, and mixes the wave functions of states (Zeeman effect). Elimination of degeneracy and the temperature-dependent occupation of states leads to the formation of a temperature-dependent magnetic moment of the ion. The magnetization of M is calculated as the statistical sum of the moments of individual m ions.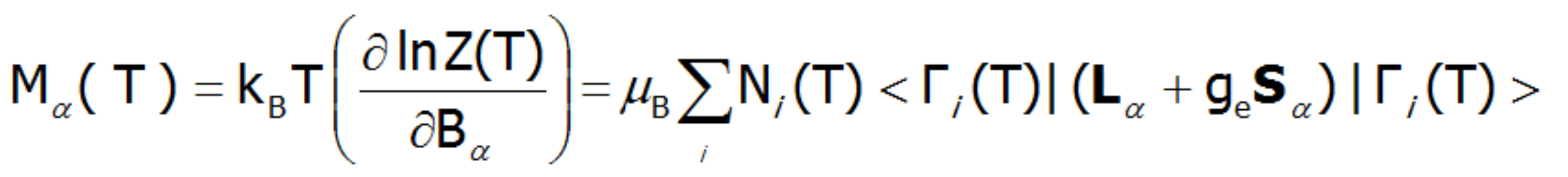
M[μ B/ f.u.] ( 1μ B = 9.27 ·10-24 J/T, J/T = A × m2 )
where:
α= x, y, z.
μB–Bohr magneton, ![]()
gL= Landé g-factor
kB-Boltzmann constant= 1,38 · 10 -23 J/K
MAGNETIC SUSCEPTIBILITY
The magnetic susceptibility of a paramagnetic state is calculated in accordance with its definition as the ratio of induced magnetization to the applied magnetic field. Taking into account the relationship between the thermodynamic functions, we can relatively simply calculate the directional components of the temperature dependence of magnetic susceptibility of a strongly correlated electron system in an unclosed shell in a crystal structure. Within the limit of low external fields, susceptibility is defined as the product of: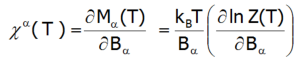
Where the -α index is the direction of the local coordinate system associated with the quantization axes in the crystal field with a certain symmetry. Bearing in mind the relationships described in the section THERMODYNAMICS OF MULTIELECTRON SYSTEMS, the matrix elements between different states are obtained within the limit of small fields:
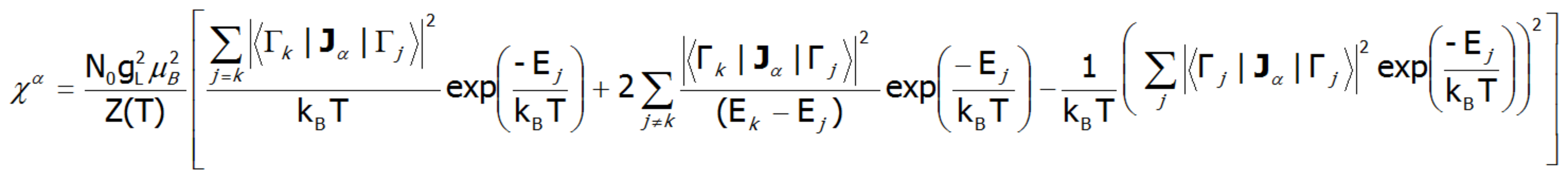
where j, k numbers the eigenstates of the Hamiltonian. For high temperatures and very weak crystal fields, this expression is reduced to the Curie law susceptibility. At temperatures comparable to the magnitude of the splitting of the states of crystal fields, these susceptibility curves may differ significantly from the shape of hyperbole. In the case of crystal fields with low symmetry, the magnetic susceptibility will exhibit a significant anisotropy. In a cubic structure, χx(T)= χy(T)= χz(T). Magnetic susceptibility can be calculated for any external fields as the ratio of the magnetization taken as the sum of the induced magnetic moments to the applied field. Due to the often observed non-linear increase in the value of the magnetic moment, the susceptibility calculated for different fields may vary considerably.
SPECTROSCOPIC OBSERVABILITY OF INTERSTATE TRANSITIONS
Fine electron structure is observed in a number of spectroscopic methods (EPR ESR, IR spectroscopy, Raman scattering, etc.). Currently, the best method for exploring the fine electron structure is Inelastic Neutron Scattering (INS). For a system of N identical ions, a differential cross section in the INS experiments is assumed as follows: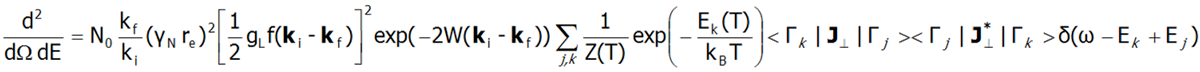
In the above equation γN is the gyromagnetic factor of the neutron, re is the classical radius of the e electron re=e2/(mec2)=2.818·10-15m, ki and kf are the wave vector of the incident and reflected neutron, respectively, and the expression exp(-2W(ki-kf)) represents the Debye-Waller factor, which describes the thermal excitation of vibrations in atoms. The delta functionδ (ω - Ej+Ek) corresponds to infinitely narrow crystal field states and is often replaced in exact calculation with the Lorentz distribution with specified half widths at half maximum (FWHM) of CEF states. The square of matrix elements from the above equation, symbolically denoted as <Γk|J┴|Γj>2 in the case of a polycrystalline material for dipole transitions is replaced with:
![]()
In the case of a single crystal, the intensity of neutron scattering for dipole transitions between CEF states (Γj and Γk) is represented by the following equation:![]()
where θ is the angle between the neutron beam and the quantization axis z.
INS is a very powerful tool for experimental verification of the theoretically calculated fine structure of electron states. Note, however, that not all CEF states are visible using this technique; only the transitions between states, where |<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| is non-zero.
SCHOTTKY SPECIFIC HEAT
Schottky specific heat occurs when dealing with a low-energy structure of discrete electron states. All we need to determine whether a given atom will exhibit the Schottky anomaly is knowledge of the electron structure of the element, i.e. the way in which electrons are arranged in shells, subshells and orbitals of the atom. In particular, the existence of fine electron structure with close lying energy levels ensures that the contribution cShottky is recognizable in the observed cShottky(T) relationships:
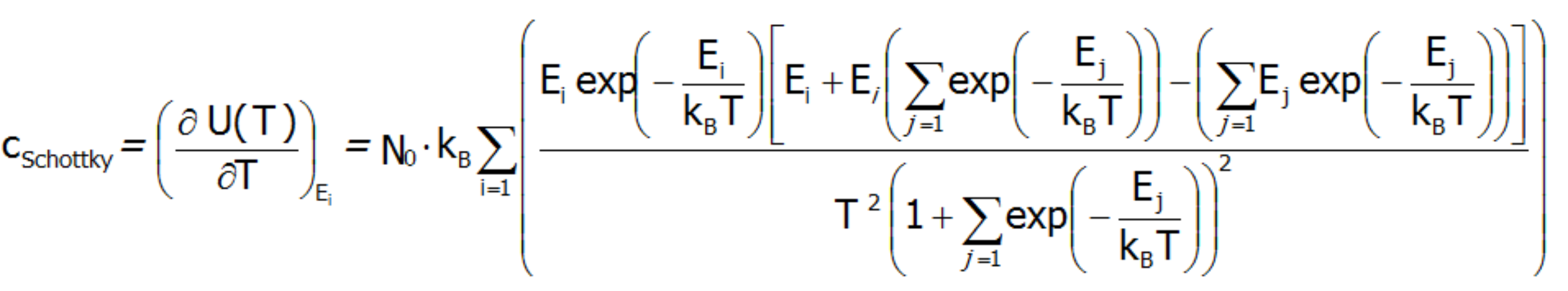
The Schottky anomaly curve is characterized by one or more peaks. Knowing the shape of this curve, we are often able to use it to determine the system of energy levels of a chemical compound. The disadvantage of this method is that we may find a number of different systems of energy levels that correspond to a single curve. Molar specific heat for localized electron system can be also calcualated difectly, as a second derivative of the Helmholtz free energy:
![]()
CRYSTAL LATTICE SPECIFIC HEAT
In order to present a realistic form of the total heat capacity of the crystal defined by paramagnetic ions and the CEF potential, we have introduced the ability to visualize the course of temperature dependence of the total heat of a crystal lattice combined with the Schottky anomaly. The heat of the lattice is simulated with the best-known and most widely accepted formal model which is based on the phonons-quantized thermal vibrations of the crystal lattice. Such vibrations can be interpreted as normal modes of harmonic oscillators and their energy determined. The energy of a single phonon is:![]()
A phonon is a quantum of vibration energy of the crystal lattice. Phonons may differ in frequency; therefore, to calculate the total energy of the lattice, the following must be performed: determine the number of phonons with a specific frequency, multiply it by the energy of a phonon with such frequency, and then sum the energies obtained for different frequencies.
The average number of phonons with a specific frequency can be determined using Bose-Einstein statistics (the so-called Bose-Einstein distribution), given by the formula: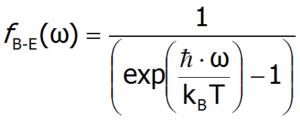
Knowing what frequency phonons of a solid can have, we can determine its total lattice energy, but for simplicity, the Debye model can be successfully used when considering phonon heat. If the length of the carbon chain consisting of N atoms in a one-dimensional lattice is denoted as L, it is possible to calculate the wavelengths using the following formula:![]()
The number of vibrations in the lattice are calculated by converting the above formula to the one below:![]()
In three-dimensional space, the number of vibrations with a certain frequency is calculated similarly, although the formula will have additional adjustments for fixed coefficients: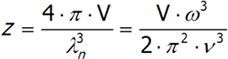
where v is the speed of sound in a vacuum, V is the volume of the crystal and ω is the frequency. The last equation is differentiated from ω.We will have reached the full number of vibrations of N atoms with three degrees of freedom, each computed by integrating the above expression: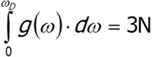
Not all vibrations are allowed in the Debye model, so integration must be performed from zero to ωD, which is maximum frequency of normal mode that may occur in the crystal. ![]()
Let us calculate ωD using the last equation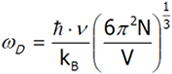 [9]
[9]
multiply both sides of the equation by
![]()
![]() [9]
[9]
| ||||||||||||
Table Debye temperature for several selected elements in the solid phase |
The resulting equation defines the Debye temperature (Θ), which is the temperature at which no new normal vibrations occur in the crystal. The Debye temperature also determines the crystal's behavior at a given temperature and how to calculate its specific heat (depending on the temperature).
If the temperature of the crystal is lower than Θ, its oscillation amplitude increases and new vibrations arise. At a temperature higher than Θ, the amplitude continues to increase, but new vibrations no longer arise. Table above shows the values of the Debye temperature for several elements .
To derive the formula for the Debye heat, we must first calculate the internal energy, and then differentiate it from temperature. For the sake of simplicity, let us assume that the phonon velocity does not depend on its polarization. Moreover, in order to calculate the total heat energy, calculate the internal energy of one polarization and multiply it by three. 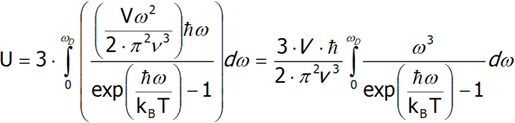
Differentiating the last equation from temperature, we shall calculate the heat capacity.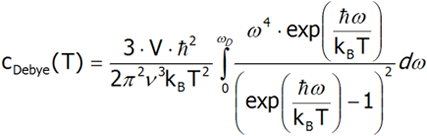
The above equation can be simplified by substituting the variables:
Eventually, the expression for the Debye heat takes the form: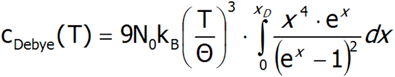
This form of the formula for the specific heat of the crystal lattice is used as a comparative in calculations that appear in the result package in the tab associated with specific heat, where by defining the value of Θ (in K units), we can observe the total heat of the crystal lattice with the Schottky anomaly (provided, of course, it is within a defined temperature range).
BIBLIOGRAPHY
- Elliot, K.W.H. Stevens, Proc. Roy. Soc.A215 (1953) 437.
- Elliot, K.W.H. Stevens, Proc. Roy. Soc.A218 (1953) 553.
- M.T. Hutchings, Solid State Phys. 16 (New York 1964 ) 227.
- Fulde in: Handbook on the Physics and Chemistry Rare Earth, Vol. 2North-Holland. Inc. (1979).
- R.J. Radwanski, N.H. Kim-Ngan, F.E. Kayzel, J.J.M Franse, D. Gignoux, D. Schmitt, F.Y. Zhang, J. Phys.: Condens. Matter 4 (1992) 8853.
- A broad description of the analysis of the thermodynamics of systems can be found e.g. in: K. Huang, Statistical Mechanics, John Wiley and Sons, Inc. New York (1963).
- Rudowicz, J. Phys. C: Solid State Phys. 20(1987) 6033.
- R.J. Radwański, Z. Ropka & R. Michalski in: Magnetism and Electronic Correlations in Local-Moment Systems: Rare Elements and Compounds, edited by M. Donath, P.A. Dowben & W. Nolting, World Scientific (1998) 445-453
- Kerson Huang Podstawy fizyki statystycznej PWN 2006; Tłumaczenie: Magdalena Załuska-Kotur
- P.W. Atkins Chemia Przewodnik po chemii fizycznej PWN 1997

