POINT CHARGE MODEL (PCM )
The point charge model is a simplified model of a crystal lattice in which ligands are presented as charged spheres with a uniform surface charge distribution that excludes the screening effects of the outer shell. This allows us to determine the Amn coefficients, which is equivalent to specifying the potential at a given point (i.e. in our case, the potential energy acting on the central ion). The coefficients are introduced due to the fact that the:
![]()
where: Xi, Yi, Zi – ligand coordinates, X,y,z – position of the central ion electron. By expanding it into a Maclaurin series
![]()
we will have reached an expansion whose coefficients are in line with our Amn parameters. The potentials for the three basic symmetries will have the following form:
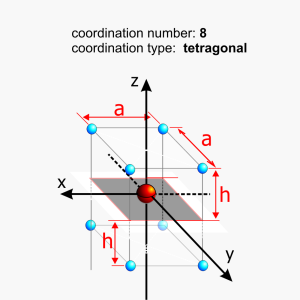
- The potential of charges in the corners of the square away from the plane
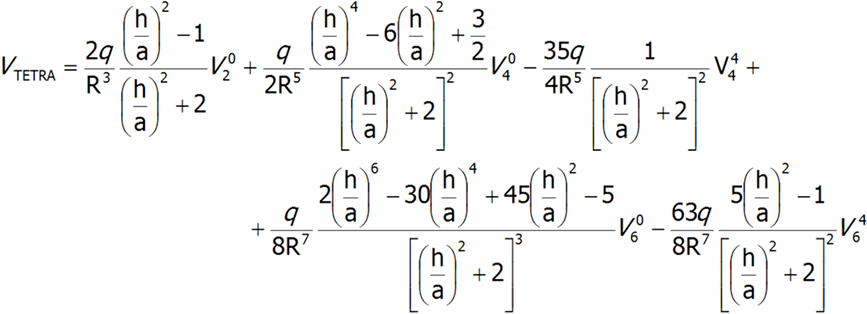
Upon rotating the coordinate system by 45°, the signs of sections V44 and V46 are altered
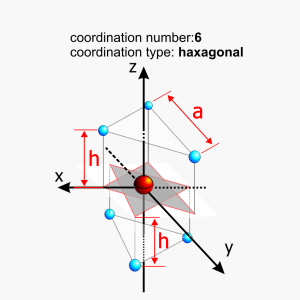
- The potential of charges located in the corners of a remote equilateral triangle
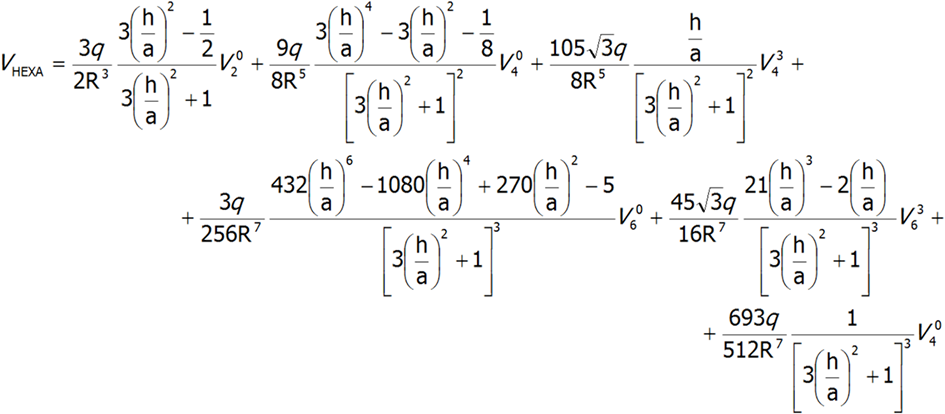
Upon reflecting in the horizontal plane, the signs of sections V34 and V36 are altered
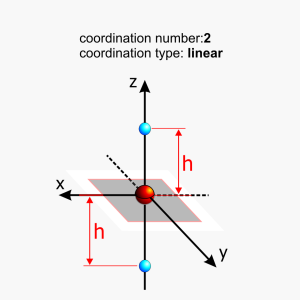
- The axial potential of a point charge
![]()
By rotation and superposition of these three components, we can compose the symmetry of the most highly symmetrical potentials carried by ligands in crystals.