MAGNETIC INTERACTIONS
A logical starting point to discuss the magnetic properties of an ion in a crystal field is to present the primary properties of strongly correlated multi-electron states of an unclosed shell, which in turn boils down to analysis of multi-electron wave functions. However, due to the different properties of the structure of the states, magnetic ions must first be divided into those whose unclosed shell contains an odd number of electrons (Kramer ions), and those with an even number of electrons (non-Kramer ions). The need for such a distinction is due to the fact that the degeneracy of the multiplet states can only be completely eliminated in the case of non-Kramer ions whose crystal field has sufficiently low symmetry. In the case of Kramer ions, a crystal field of any low symmetry cannot eliminate the degeneracy; at most, it can only split the multiplet to create so-called Kramer doublets. Calculation of the CEF provides the structure of electronic states with eigenfunctions being combinations of z-fold components of the total momentum of an unclosed shell. The basis of Hamiltonian eigenfunctions allows the expected value of the magnetic moment of each state based on the knowledge of the wave function to be found. In the absence of a magnetic field, multiplet states partially split by a crystal field do not have a magnetic moment. In the case of a Kramer ion, lack of a specific magnetic moment is always caused by a full compensation of the magnetic moments of degenerate magnetic states. However, when we apply any small external magnetic field, degeneration is eliminated and a nonzero magnetic moment of the split states appears. In the case of non-Kramer ions, the lack of magnetic moment of singlet states is the result of the shape of the wave function. In accordance with the basic approach, singlet states of a non-Kramer ion do not interact with the applied magnetic field, although careful analysis of the specific situation may lead to the opposite conclusion. Positive magnetic susceptibility of atoms occurs only when the atom has at least one unclosed electron shell. According to the quantum theory of magnetism, the magnetic moment of an electron system consists of orbital momentum and spin momentum:
where i means summing electrons and gl =1, ge =2.002324.
For atoms with a specific angular momentum of the entire electron shell J, the magnetic moment of this shell is proportional to J and is presented by a vector expression:
To calculate the effect of an external magnetic field on the paramagnetic ion (only if J is a good quantum number) located in the crystal lattice, add a Zeeman section to the CEF Hamiltonian. Bear in mind that the change in the energy of a state in a magnetic field δE = -m•B, and that:
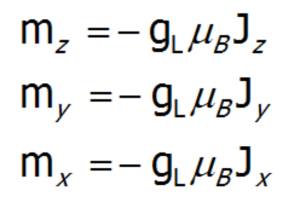
a single-ion Hamiltonian of an ion in basis |J,Jz> in an external field will be as follows:
Similarly, for the basis |L, S, Lz,Sz>, a full Hamiltonian with molecular magnetic field interactions (e.g. Mean Field Approximation) will take the form:
It should be emphasized that, depending on the direction of the applied external field, in general cases different magnetic properties of the ion are acquired due to the symmetry of the environment with respect to the local coordinate axes. Therefore, in order to calculate the impact of various direction components of the external field, in place of the symbolically expressed J•Bzew in the Hamiltonian realized on basis of |J,Jz>, JzBz, JxBx and JyBy are calculated separately.
For all considerations, it is important to emphasize that both the Hamiltonian CEF component and the Zeeman component are diagonalized as a whole (simultaneously), which in turn establishes the interactions between the different CEF states in nonzero magnetic fields.
All the previous considerations refer to the magnetic properties of non-interacting paramagnetic ions. However, the presented approach takes into account the interchangeable magnetic interactions between paramagnetic ions. The basic idea behind these calculations is based on the approximate molecular field. To simplify the discussion, calculations for the molecular field are presented for the "small basis" |J,Jz> (the reasoning for the full basis |L, Lz, S,Sz> is similar). If we replace the external field in a Zeeman section of a Hamiltonian with an internal molecular field derived from magnetically identical neighbors in the crystal lattice, they can be represented as follows:
where <J> represents the average temperature of the total angular momentum vector of the shell. The molecular field coefficient, nmol, quantitatively describes the ratio of the molecular field in the place of the magnetic ion to the magnetic moment of the ion that is its source. Due to the fact that all paramagnetic ions in a crystal lattice are identical, they all interact in an identical manner. Changing the energy of the i-th state of the paramagnetic ion in the magnetic field derived from external ions is therefore equal to:
where Ji is the vector of angular momentum associated with each CEF state. Such a definition of a molecular field allows a Hamiltonian that contains self-aligning interactions to be built. The paramagnetic ion is a source of the magnetic field, because a magnetic moment is induced on it that is caused by magnetic fields derived from other ions with momentum induced by the following ions. While constructing a self-aligned Hamiltonian of the 4f ion, one must be careful not to calculate the energy of magnetic ions as a sum of energy of the individual ions. It must be remembered that although all states change their energy, some energy is associated with the field itself (similar to the energy of the capacitor and the magnetic energy of the coil with a current). The total energy of the system of ions is thus determined by the energy of individual ions in the molecular field reduced by the energy of the magnetic field they produce [6]:
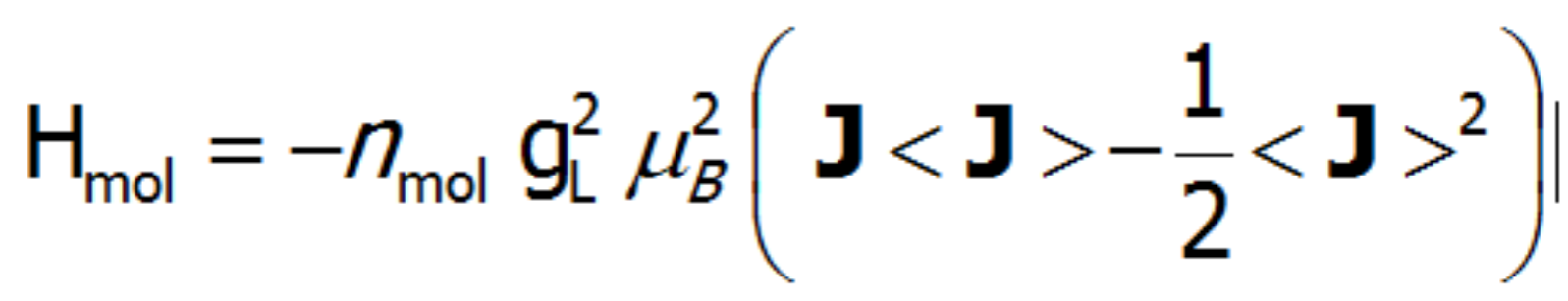
Having defined the sections of the Hamiltonian describing the interaction of a multi-electron system with a crystal field, molecular, magnetic field interactions (Mean Field Approximation), and the interaction with the external magnetic field, we can finally present the whole Hamiltonian implemented on the basis of |J,Jz>:
This includes both single-ion and interionic sections, which in the case of numerical calculations allows for simultaneous diagonalization of all sections at each temperature step. This makes it possible to define eigenenergy and directional components of the total angular momentum in an unclosed shell for individual eigenstates Γi, calculated as the square values of wave functions in angular momentum representation. In practice, the solution to the eigenequation of the described type of Hamiltonian boils down to diagonalization of the matrix (2J+1)·(2J+1), which obviously leads to reaching the energy value of 2J+1 states. Taking into account that:
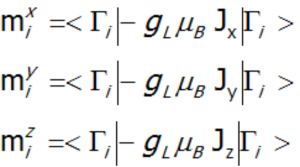
each (i-th) state of the fine structure can be related to its magnetic moment (where: gL – Landé g-factor).
MAGNETIC MOMENT AND MAGNETIZATION
In the applied methodology, calculating the magnetization boils down to summing the identically behaving magnetic moments of individual ions with an unclosed electron shell. Due to the fact that rare earth ions are in a self-aligned molecular field, their magnetic moment value changes with temperature. Bearing in mind that each eigenstate of the CEF Hamiltonian is related to its magnetic moment, the total moment of a strongly correlated electron system at a given temperature is the resultant moment of occupied states calculated with the inclusion of the Boltzmann weight: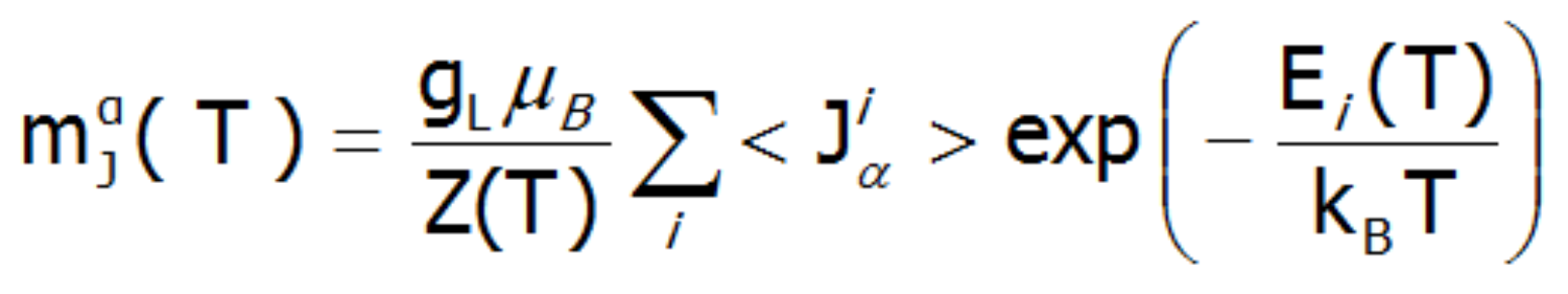
In the above equation, the α index is a directional component, i numbers the Hamiltonian eigenstates, while <Jiα> represents the expected value of the total angular momentum on the α axis in the i-th state. It should be emphasized that at T = 0, when only the ground state is occupied, the magnetization of the ion system 4f per 1 ion is equal to the expected value of the magnetic moment of the ground state. Due to the fact that all ions behave identically in this model, the calculated temperature dependence of the magnetic moment is closely linked to the value of the molecular field, which is:
The value of the molecular field factor, nmol, determines the temperature at which the magnetic order Tc occurs. Calculations of magnetization in the ordered state allow the magnetocrystalline anisotropy of the system to be determined. In the case of tetragonal symmetry, the expansion of the anisotropy energy can be represented in a known form:
where Ki(T) are coefficients of anisotropy dependent on the temperature, and θ and φ are polar angles describing the direction of the magnetic moment relative to the perpendicular crystallographic axes. The coefficients Ki(T) are closely related to the parameters of the crystal field. In a field with tetragonal symmetry, they have the following value: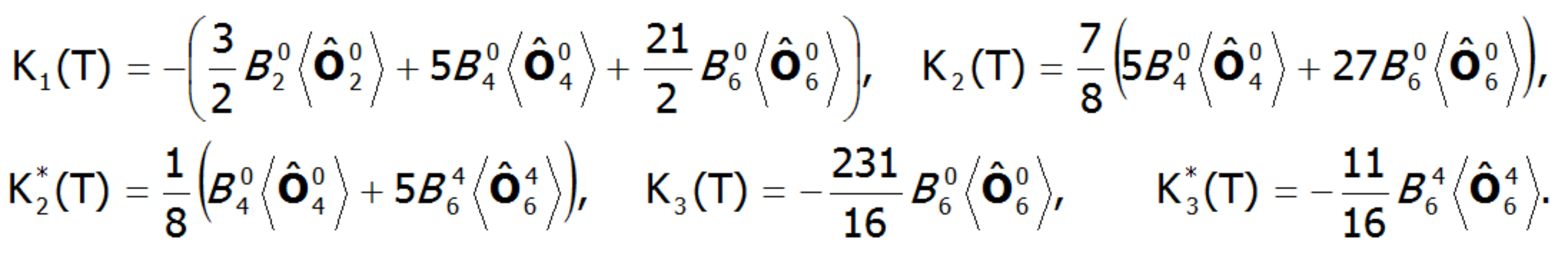
where: 
represents the average temperature of Stevens operators. The possibility of calculating the value of induced magnetic moments in an external field applied in different directions makes possible the direct determination of magnetocrystalline anisotropy. This approach can clearly determine the components of the total magnetic moment of paramagnetic ions. The total magnetic moment of the ion consists of the orbital and spin sections: mc=mL+mS. Knowledge of the expected values of the momentum vector components of each state <Jiα> makes it possible to specify the share of the spin and orbital sections of the magnetic moment. Bearing in mind that:
and taking into account that gl = 1 and gs = 2.002324:
we will have reached:
The above relationships indicate that the ratios of each component of the magnetic moment to the total momentum are fixed for a given ion and independent of their environment and temperature:
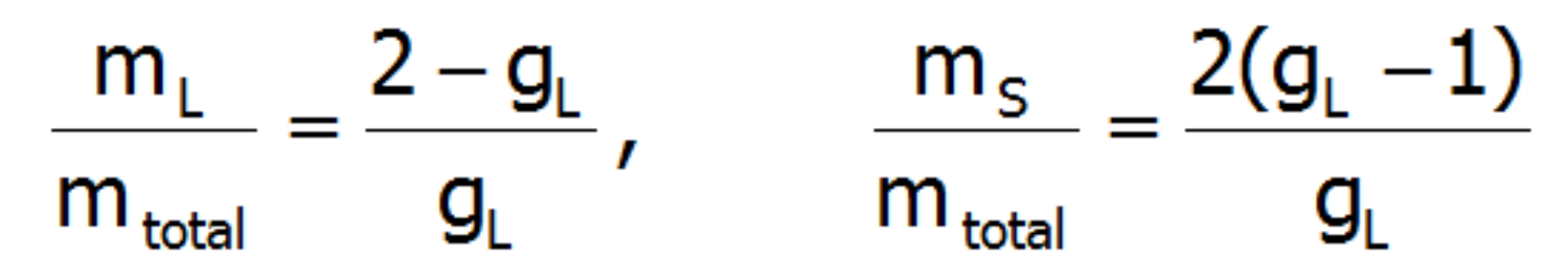
The issue of the accuracy of the above reasoning is discussed at the beginning of the description of the theoretical bases of the application. Results of calculations performed on the basis of |J,Jz> provide states of lowest multiplet. The fuller basis of |L,S,Lz,Sz> takes into account the coupling between the states of different multiplets. Determining the value of the orbital and spin components of the magnetic moment of the paramagnetic ion with an electron structure calculated in the representation |L,S,Lz,Sz> boils down to a simple interpretation of the expected values L and S.
An external magnetic field eliminates the degeneracy, changes the energy value of the states, and mixes the wave functions of states (Zeeman effect). Elimination of degeneracy and the temperature-dependent occupation of states lead to the formation of a temperature-dependent magnetic moment of the ion. The magnetization of M is calculated as the statistical sum of the moments of individual m ions.
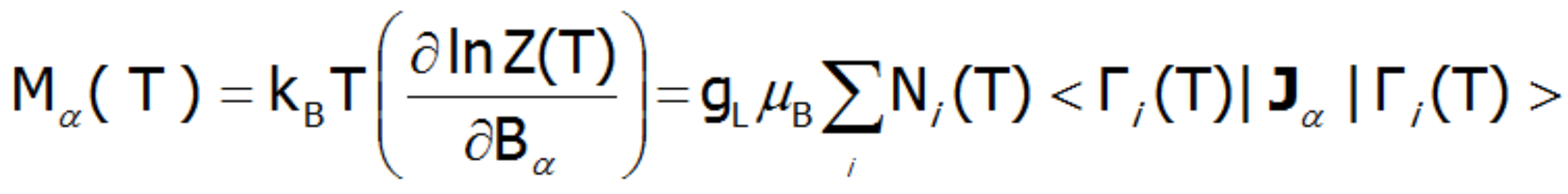
where: α= x, y, z. μB–Bohr magneton:
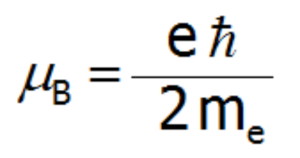
where: gL – Landé g-factor, kB- Boltzmann constant= 1,38 · 10 -23 J/K
MAGNETIC SUSCEPTIBILITY
The magnetic susceptibility of a paramagnetic state is calculated in accordance with its definition as the ratio of induced magnetization to the applied magnetic field. Taking into account the relationship between the thermodynamic functions, we can relatively simply calculate the directional components of the temperature dependence of magnetic susceptibility of a strongly correlated electron system in an unclosed shell in the crystal structure. Within the limit of low external fields, susceptibility is defined as the product of: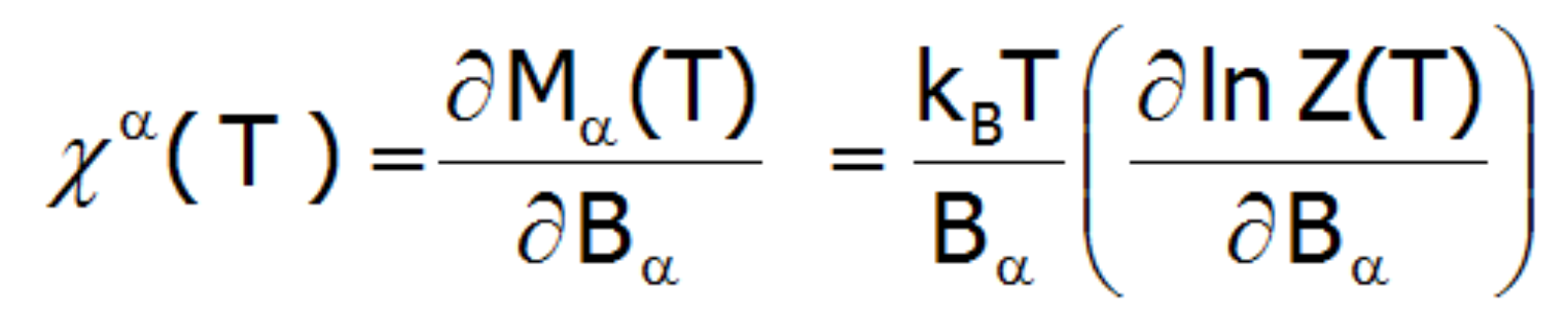
Where the -α index is the direction of the local coordinate system associated with the quantization axes in the crystal field with a certain symmetry. Bearing in mind the relationships described in the section THERMODYNAMICS OF MULTI ELECTRON SYSTEMS, the matrix elements between different states are obtained within the limit of small fields: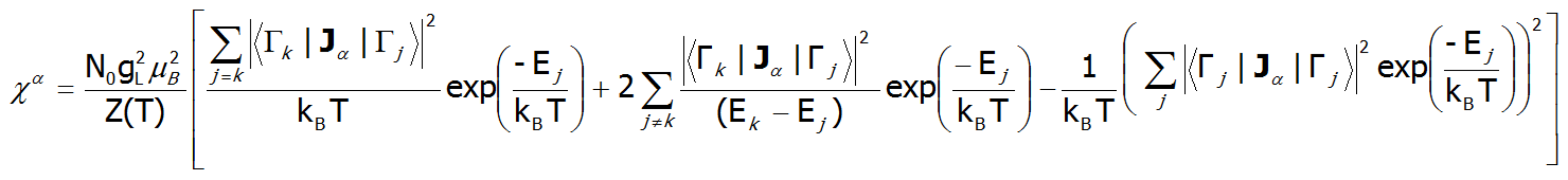
where j, k numbers the eigenstates of the Hamiltonian. For high temperatures and very weak crystal fields, this expression is reduced to the Curie law susceptibility. At temperatures comparable to the magnitude of the splitting of the states of crystal fields, these susceptibility curves may differ significantly from the shape of a hyperbole. In the case of crystal fields with low symmetry, the magnetic susceptibility exhibits a significant anisotropy. In a cubic structure, χx(T)= χy(T)= χz(T). Magnetic susceptibility can be calculated for any external fields as the ratio of the magnetization taken as the sum of the induced magnetic moments to the applied field. Due to the often-observed non-linear increase in the value of the magnetic moment, the susceptibility calculated for different fields may vary considerably.
SPECTROSCOPIC OBSERVABILITY OF INTERSTATE TRANSITIONS
Fine electron structure is observed in a number of spectroscopic methods (EPR ESR, IR spectroscopy, Raman scattering, etc.). Currently, the best method of exploring the fine electron structure is Inelastic Neutron Scattering (INS). For a system of N identical ions, a differential cross section in the INS experiments is assumed as follows: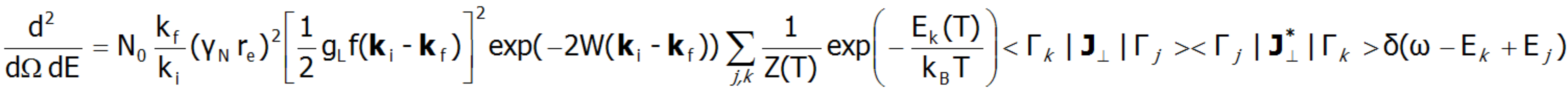
In the above equation γN is the gyromagnetic factor of the neutron, re is the classical radius of the e electron re=e2/(mec2)=2.818·10-15m, ki and kf are the wave vector of the incident and reflected neutron, respectively, and the expression exp(-2W(ki-kf)) represents the Debye-Waller factor, which describes the thermal excitation of vibrations in atoms. The delta function δ (ω - Ej+Ek) corresponds to infinitely narrow crystal field states and is often replaced in exact calculation with the Lorentz distribution with specified half widths at half maximum (FWHM) of CEF states. The square of matrix elements from the above equation, symbolically denoted as <Γk|J┴|Γj>2 in the case of a polycrystalline material for dipole transitions is replaced with [20]:
In the case of a single crystal, the intensity of neutron scattering for dipole transitions between CEF states (Γj and Γk) is represented by the following equation: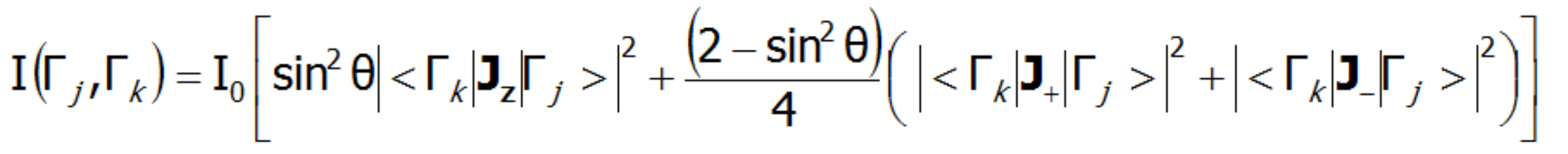
where θ is the angle between the neutron beam and the quantization axis z. INS is a very powerful tool for experimental verification of the theoretically calculated fine structure of electron states. Note, however, that not all CEF states are visible using this technique - only the transitions between states, where: |<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| is non-zero.
