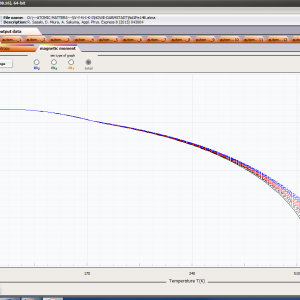
All ATOMIC MATTERS calculations can simulate materials under stable field conditions (both CEF and external magnetic field) and interactions. ATOMIC MATTERS MFA can simulate phase transitions of ionic/atomic systems according to dynamic calculations of the molecular field Bmol, simply defined as:
![]()
that interacts with ions to induce their magnetic moment. Such self-consistent calculations can be performed after establishing the molecular field factor nmol, which is closely related to the phase transition temperature (TC or TN). Our solution applies to situations in which an unclosed electron 3d/4d/5d/4f/5f subshell interacts with the electrostatic potential of definable symmetry (taken as a CEF) and the external magnetic field and molecular magnetic field of identical neighbors, calculated under Mean Feld Approximation (MFA) methodology.
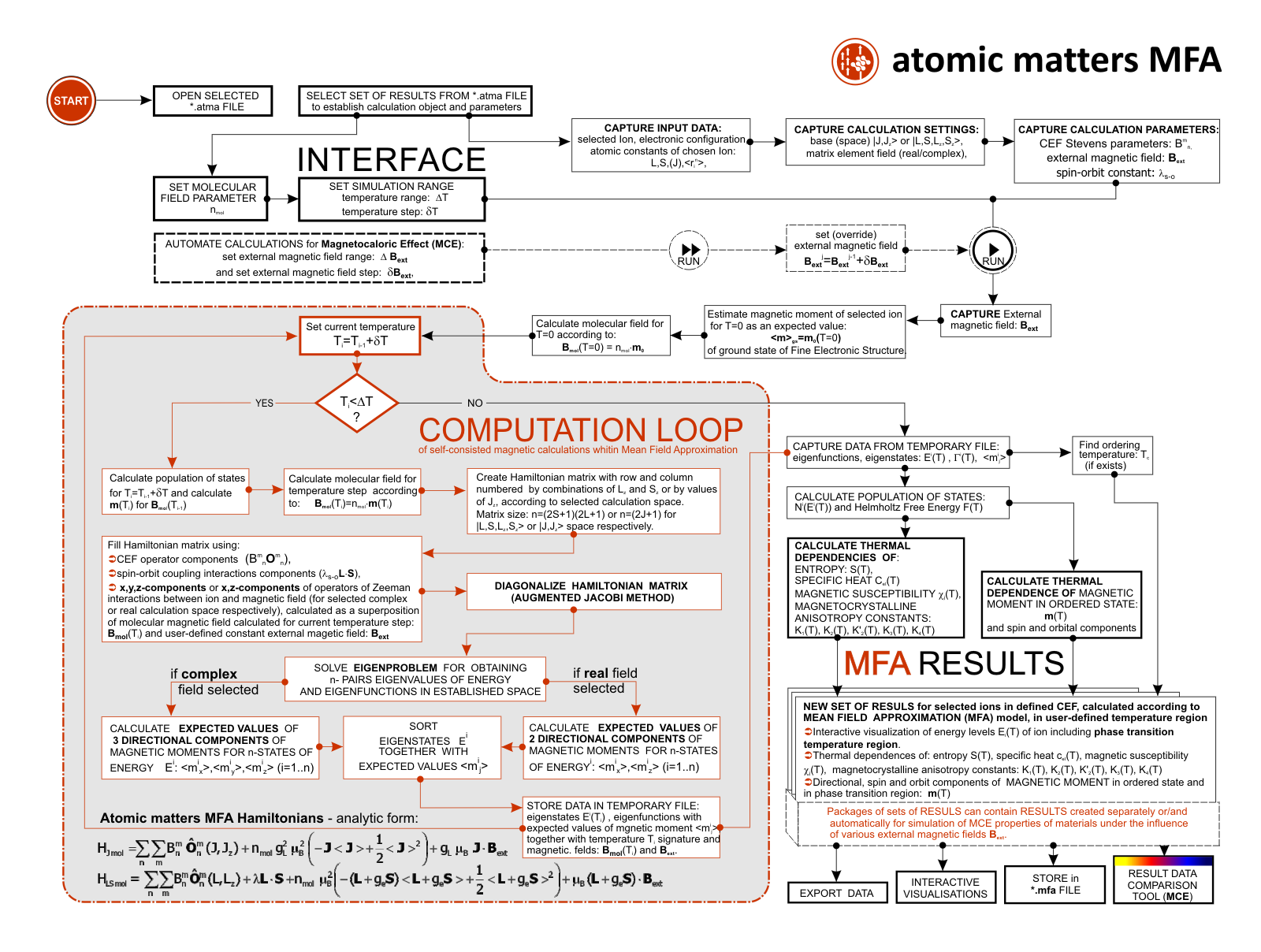
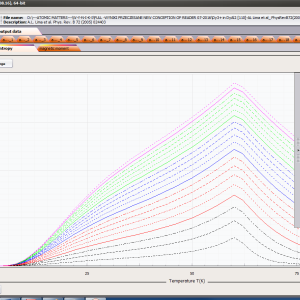
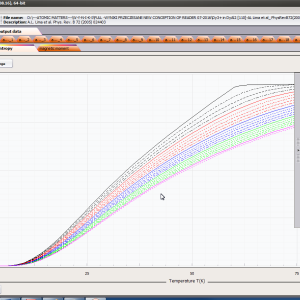
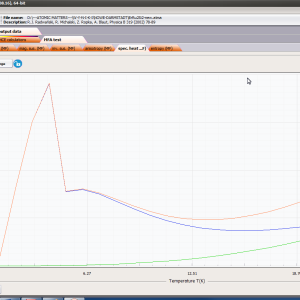
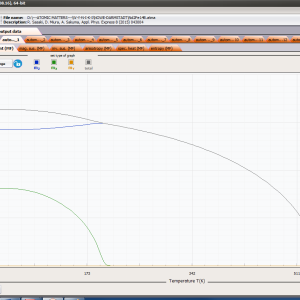
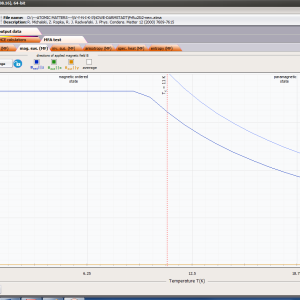
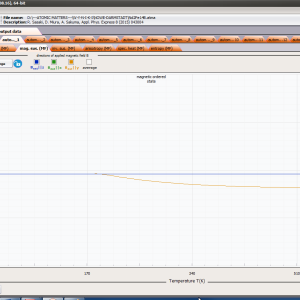
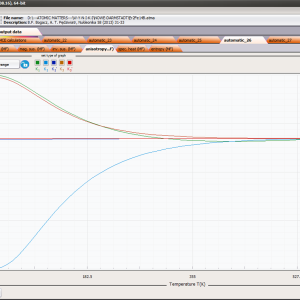
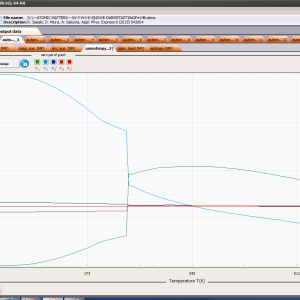
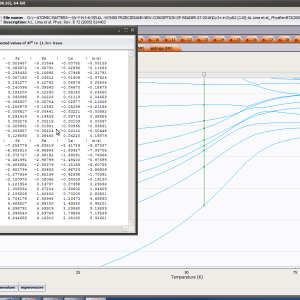
ATOMIC MATTERS MFA computation systems is based on self-consistent methodology of MFA. Taking into consideration the individual population of states of fine electronic structure of ions/atoms different temperatures according L. Boltzmann statistics makes it possible to define the temperature dependencies of properties such as:
- full structure of discrete electron levels (T) for magnetization process in chosen calculation space |J,Jz> or |L,S,Lz,Sz>
- Helmholtz free energy F(T)
- internal energy U(T)
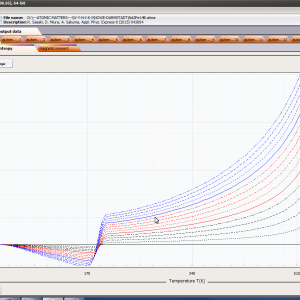
- magnetic entropy Smag(T)
- formation of magnetic ordered state
- localized electronic contribution to specific heat c(T) both: for stable energy levels for structure Ei and for magnetic phase transitions
- spectra simulations for different methods and conditions, including INS (Inelastic Neutron Scattering)
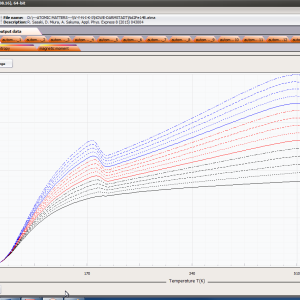
- magnetic moment and magnetization in ordered state
- spin and orbital contribution to angular momentum of the entire electron subshell;
- magnetocrystalline anisotropy constants Ki(T)
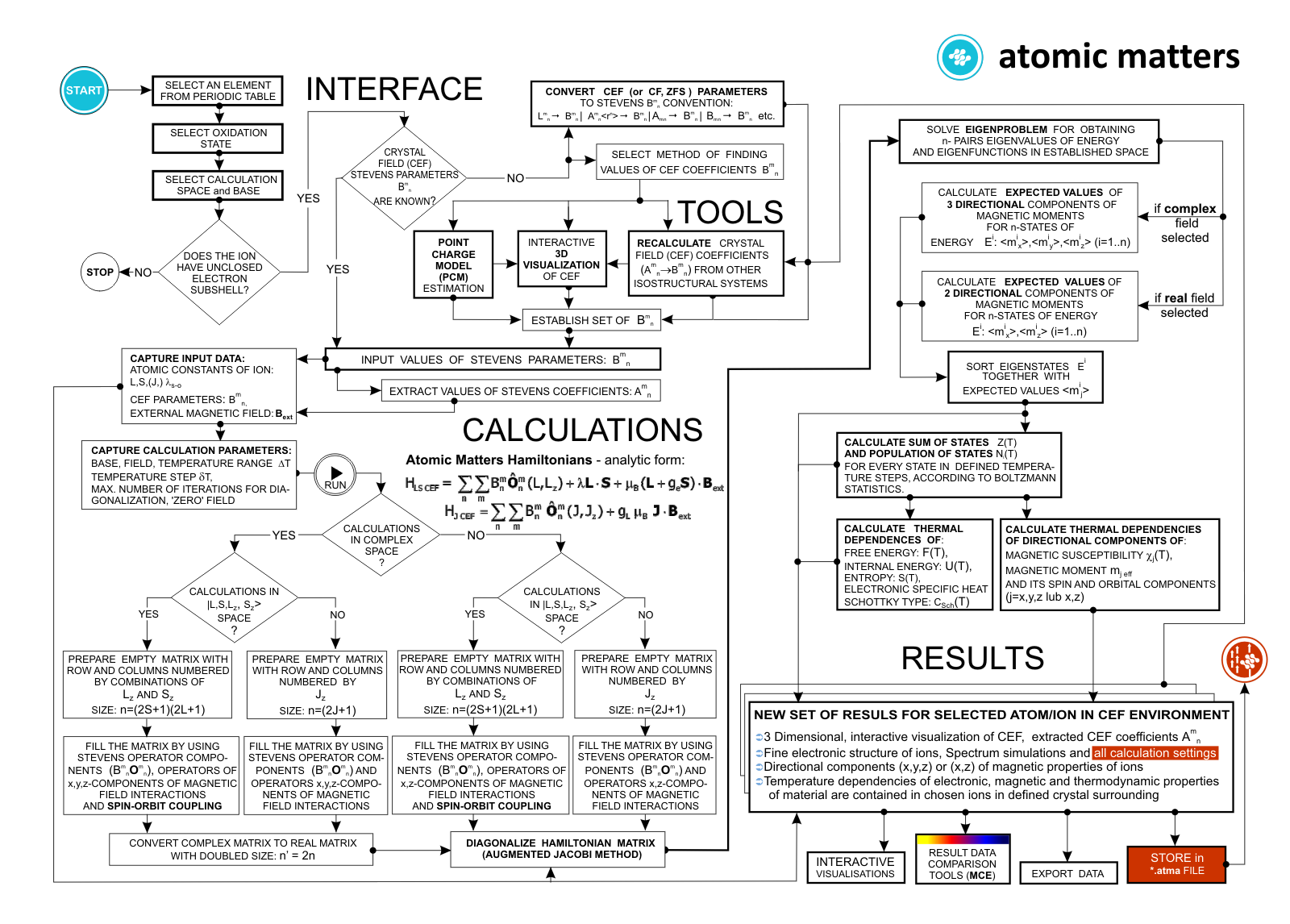
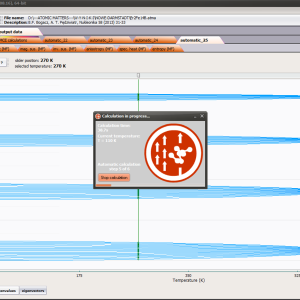
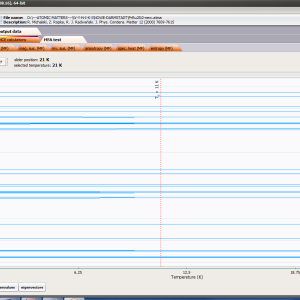
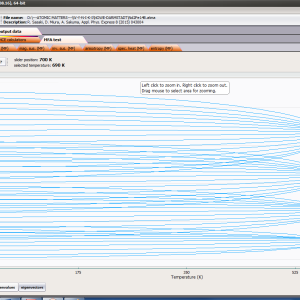
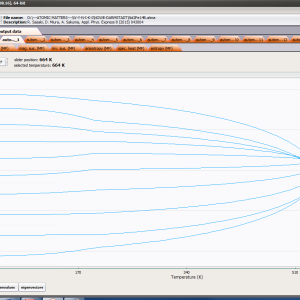
For rapid calculations in the thermodynamically stable temperature region, ATOMIC MATTERS offers the following CEF+Spin-Orbit+Zeeman Hamiltonian according to the chosen calculation space of ground multiplet |J,Jz> or ground atomic term |L,S,Lz,Sz,> respectively. For calculating properties in temperatures around the magnetic phase transition point, self-consistent methodology for molecular field calculation called Mean Field Approximations(MFA) is applied. The idea of this method is the estimation of direction and value of the magnetic field (molecular field) generated by ions at defined temperature, and calculating the influence of this magnetic field for electronic states structures of ions. According to the chosen calculation space, we define molecular field as:
![]()
or
![]()
On the basis of calculated electronic structure Ei, the directional components of magnetic moments are established for all identical ions. This means that Hamiltonian matrix diagonalization is performed for all defined temperature steps recurrently, in contrast to simple ATOMIC MATTERS calculations, which diagonalize matrices one time for a single run and deduce all thermodymamical properties from the stable discrete energy level structure obtained. This self-consistent procedure provides temperature-dependent energy level structure and has only one only free parameter, nmol, called the molecular field parameter. The value of nmol is closely related to the phase transition temperature TN or TC of the macroscopic structure of ions. The formal expression of the full Hamiltonian used by ATOMIC MATTERS MFA computation system, according cto the hosen calculation space |J,Jz> or |L,S,Lz,Sz,> respectively, has the form:
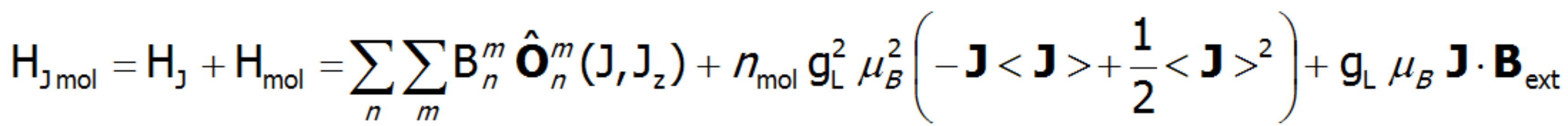
or
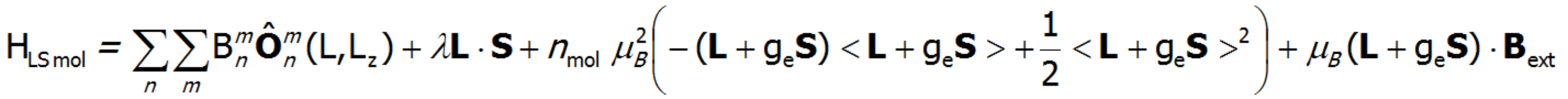
The eigenvectors of the Hamiltonian are described according to the selected calculation base by the total momentum quantum numbers |J,Jz> or spin and orbit quantum numbers |L,S,Lz,Sz,>. Using the commutation relations of the angular momentum operators, we obtain information about expected values of the projections of magnetic momentum of all electronic states at a chosen temperature:
![]()
or
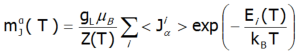
Where: α indexes directional components, i - numbers the Hamiltonian eigenstates, while <Jα> represents the expected value of the total angular momentum along the α-axis in the i-th state. MFA Hamiltonian is related to magnetic moment, the total moment of a strongly correlated electron system at a given temperature is the resultant moment of occupied states calculated with the inclusion of the Boltzmann weight and:
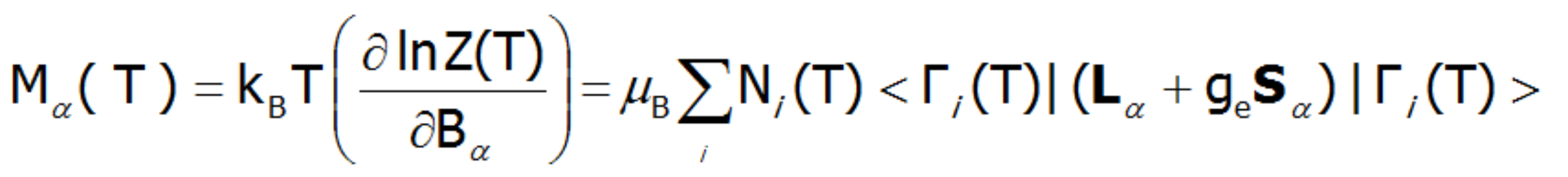
or
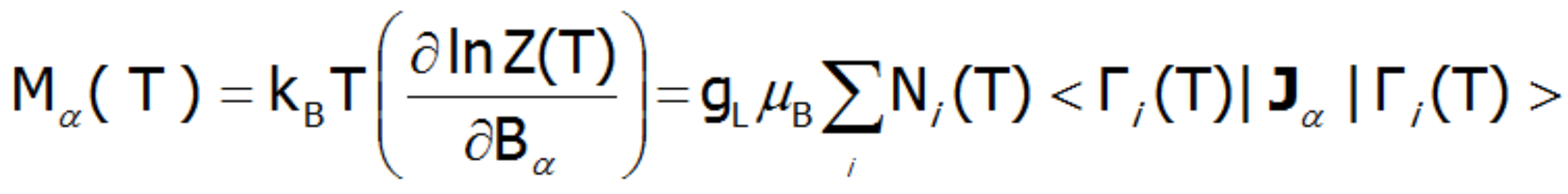
where α indexes directional components, i-numbers the Hamiltonian eigenstates, while <Jα> and represent the expected values of the total angular momentum operator defined in different spaces. Such magnetic moment calculations, under influence of a freely defined external magnetic field and internal dynamic calculated molecular field can be achieved by ATOMIC MATTERS MFA.
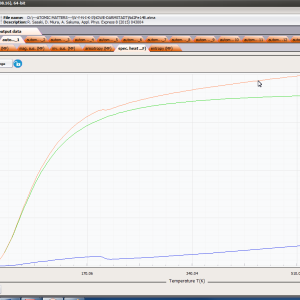
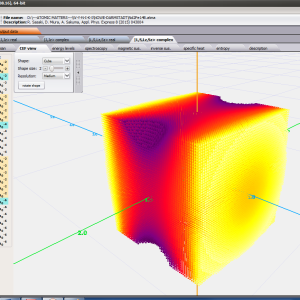
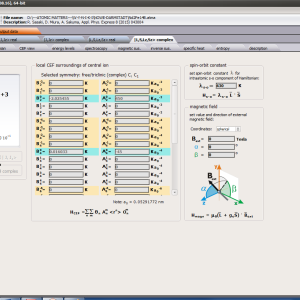
ATOMIC MATTERS MFA also provides single-ionic magnetocrystalline anisotropy calculations that include full calculations (without Brillouin function approximation) of Ki(T) magnetocrystalline constants for defined temperature ranges. . The visual form of calculation results and full 3D interactive CEF potential visualization make it easy for the user to utilize the power of the application very effectively.