ATOMIC MATTERS is a unique tool created by scientific professionals that can fully and accurately describe the physical properties of atomic electron systems subjected to electromagnetic interactions typical of situations where an unclosed electron shell interacts with electrostatic potential and magnetic fields. ATOMIC MATTERS combines a package of unique scientific tools created by professional scientists from the fields of atomic physics, solid state physics, and magnetism. ATOMIC MATTERS can predict macroscopic properties of specified materials as a result of the physical properties of atomic electron systems with an unclosed electron shell that interacts with electrostatic, multipolar potential of definable symmetry and an external magnetic field. Visual calculation results (including full 3D potential visualization), intuitive workflow, powerful tools, and comparative data make a gentle learning curve for new users. For over a decade we have been creating user-friendly software that allows a strict quantum-mechanical regime to model properties of matter whose nature is single-ionic (single-atomic). The computational methods of ATOMIC MATTERS are based on our own procedures for the generation and diagonalization of matrices (equivalent operators) with composite elements, and are in strict compliance with the conventions and methodology of modern atomic physics, solid state physics, and numerical techniques described in widely respected scientific publications.
Constantly striving for maximum simplification of the application interface, we have achieved the ability to conduct reliable research in the area of the properties of magnetic materials and prediction of properties of solid compounds without knowledge of the complexities associated with the axioms and methodology of quantum mechanics. The application logic makes it possible to forecast the magnetic, thermal and electron properties for the whole isostructural series. This means that ATOMIC MATTERS can predict the physical properties of materials whose nature is derived from localized electron states. From a practical point of view, the role of electron states for the magnetic, spectral and calorimetric properties of materials containing transition metals, rare earth metals, or uranics, is absolutely fundamental. However, there is much controversy in science over the selection of an adequate theoretical description of specific groups of chemical compounds in a solid state. Leaving aside the doctrinal manifestoes, we give you a tool for checking and comparing experimental results for actual materials with the results of theoretical calculations based on accurate quantum mechanical calculations based on the formalism of the equivalent operators theory (based on the Wigner-Eckart theorem) under the convention of Stevens operators. Users can use or eliminate specific approximations and define and decide for themselves which interactions are negligible and which are not. The diagram below shows the decision tree for an ATOMIC MATTERS user:
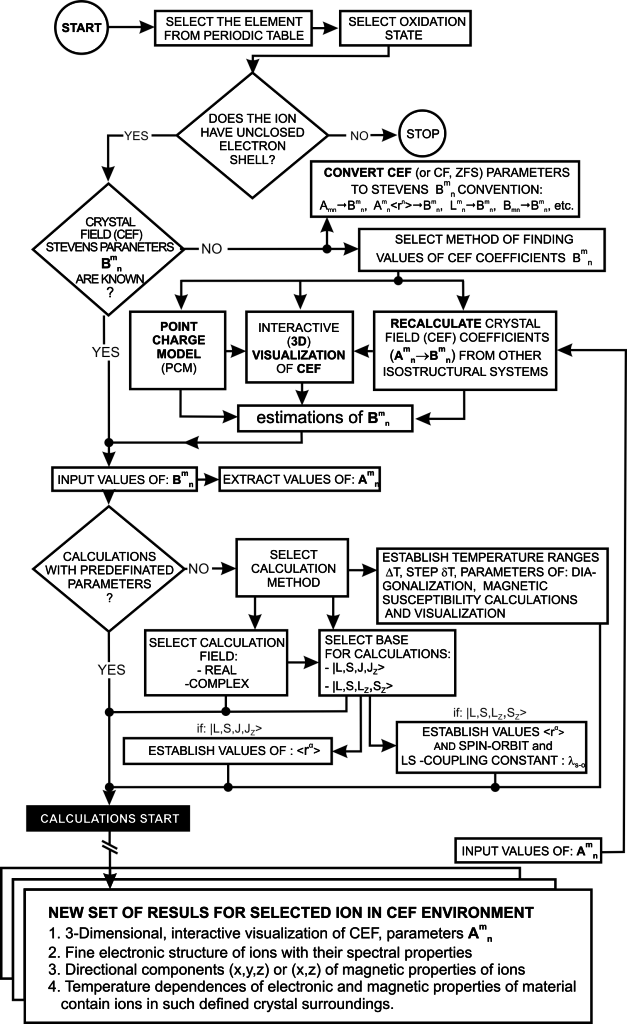
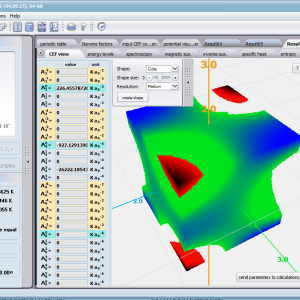
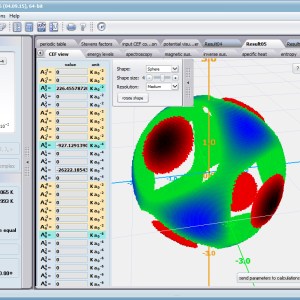
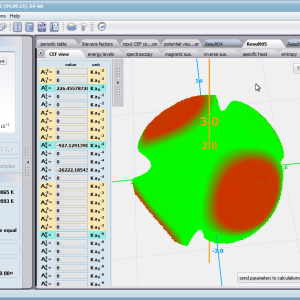
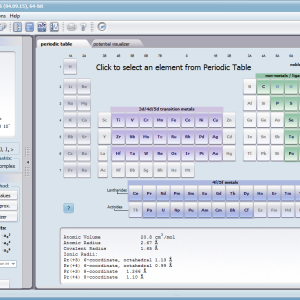
Using the latest numerical methods for diagonalization of complex Hermitian matrices in a simulated ion/atom, we have developed a program that can obtain a complete set of computational results (for typical calculations, without imposing cyclical work) within a matter of seconds on modest hardware. ATOMIC MATTERS can generate complete sets of input-output data, visualized in the form of charts, diagrams and 3D projections on sets of tabs with an intuitive, hierarchical structure. This allows for quick verification of the impact of a specific interaction on the structure of the ion/atom and the effect of this change on the macroscopic properties of the sample material. By operating on complete sets of input and output data which combine the geometry of the paramagnetic ion's environment in the crystal lattice with the properties of an ideal macroscopic crystal consisting of ions/atoms and closed-shell ions/atoms which impose no paramagnetic effect, we simulate the real properties of original materials. ATOMIC MATTERS quickly and efficiently simulates the effect of electric fields determined by a number of potential multipoles (quadrupole, octopole etc.) with defined local symmetries, and constant magnetic fields with a given direction in space, on an ion/atom with an unclosed shell (i.e. the so-called. paramagnetic ion/atom, transition metals ion/atom), arbitrarily selected from the Periodic Table of the Elements (Mendeleev's Table). In the application, areas containing elements from which calculations can be performed are highlighted in color in the periodic table on the tab that appears when the application is started. Selecting other elements in this tab accesses important information gathered in terms of usefulness to conduct calculations for the determination of the geometry of ligands in coordination compounds. The theory and mathematical computational methods associated with the distribution of the electric field surrounding the paramagnetic ion are derived from atomic physics and the theory of groups, which were formed and developed intensively during the second half of the twentieth century. The intricacy of operator calculations dedicated for space defined by the class of symmetry of the ligand field impeded the development of computational methods, which with time created simplified calculation tools (e.g. LLW diagrams - from their creators' names: Lea, Leask, Wolf, or the de Gennes formulas) adapted by research groups at centers conducting practical research in FCS. Difficulties in defining and verifying the potential of the CEF crystal field of an ion/atom and its relationship with the crystallographic structure of a crystal were solved by interactive visualization of the coordinating potential, including numerous tools to adjust the color palette and its relationship with the value of potential, visibility (extreme potentials, near-zero potentials), figure projection (cube/sphere), the position of the observer (inside, outside, zoom), etc.
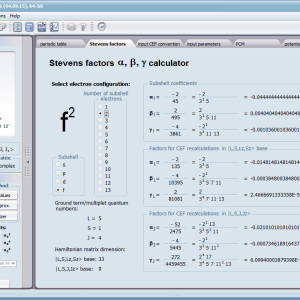
The POTENTIAL VISUALIZER tab makes it easy to view and freely compose the expansion potentials of multipole series (in the form of tesseral harmonics, later implemented computationally in a multi-dimensional space of angular momentum quantum numbers using the language of operators entered into the FCS by K.W.H. Stevens - see the theoretical basis), where, in accordance with the rules of atomic physics, the selected paramagnetic ion can be placed a set of computational results obtained for the defined crystal (as a function of temperature for a specified range). Placing various ions/atoms in the same potential can effectively simulate the properties of an entire series of compounds (provided their relative isostructurality is at least in the direct vicinity of the paramagnetic ion/atom).
A successive description of the whole series of ionic and intermetallic compounds was performed e.g. for the isostructural families of crystals: RERu2Si2, RENi5, RE2Fe14B, RBaSrCu3O7, RE2Fe14C, RE2Fe17, where Re represents a rare earth element. Numerous papers have covered such work using methodologies within the individual compounds, but without the use of an integrated environment such as ATOMIC MATTERS. Computational difficulties shifted the interest of TFCS from these methods to developing a formalism based on the concept of a crystal realized by fuzzy wave functions, which was proposed by F. Bloch and achieved considerable success in the description of transport phenomena in materials. The research experience of the authors indicates that it is possible to separate the calculations relating to conduction electrons and electrons forming unclosed shells d or f, which retain their integrity and make a fundamental contribution to the magnetic properties of the material. At the same time, the creators of the application wish to underline that single-ion properties play an important but not singular role in the macroscopic properties of the crystal. The effects associated with the domain structure and long-range interactions, or the possible dimerization or delocation is not taken into account in this approach, although they may be covered by ATOMIC MATTERS in the future.
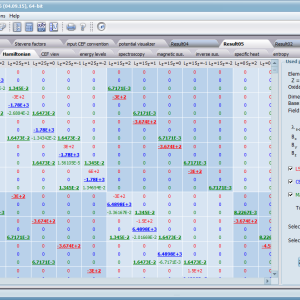
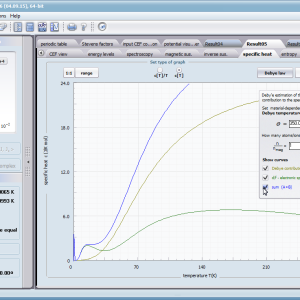
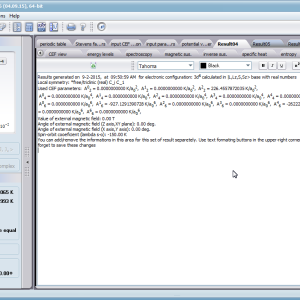
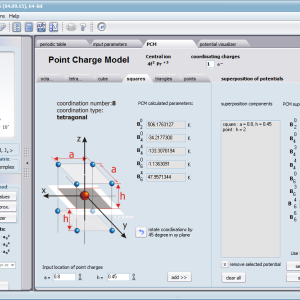
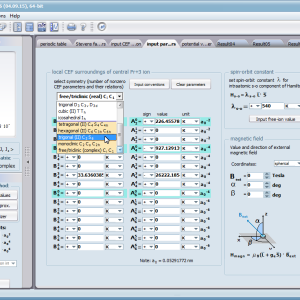
Let us therefore present an application that allows you to clearly, accurately and properly apply theoretical physics of the atom/ion subjected the effect of an electrostatic field in accordance with the concept of CEF (Crystal Electric Field, in the formalism of equivalent Stevens operators, directly defined by the Wigner-Eckart theorem), with coefficients defined in many ways (including the point charge model, or an interactive visualization in three dimensions - 3D). At every step of selecting methods or using approximations, the application sets the default selection to a standard recognized by DFCS for the ion/atom or class of issues. For constant atomic values used in the calculations, the choice of methods and parameter values is completely open and records can be kept with full freedom; you can accept the default parameters, be they table-derived or adjusted to typical computational situations (the origin of which can be documented and verified). Taking care of the complete controllability of calculations, we provide you with full control of the introduced constants, whose values can be edited in external program files together with a note on the origin of the edited constant. The ability to access the components of the generated Hamiltonian matrix for selected input parameters allows comparison of full sets of output data from multiple (up to 99) calculations, and each relationship depicted in the diagram can be completed with comparative data (e.g. experimental data, literature) entered directly via the keyboard or clipboard to a convenient, drop-down sheet hidden on the right of each tab containing temperature visualizations of the presented value. To avoid any metrological problems, the application has a handy converter of units and sizes, made in the form of thematic tabs, allowing you to quickly convert units used in all calculations and definitions between most known standards. A number of integrated tools allow the simulation, transformation, conversion, comparison and visualization of many of the properties of the canon (benchmark model) of classical solid state physics, such as Debye heat capacity, multi-level electron Schottky heat, statistical entropy, Curie's law, and many others.
ALGORITHM
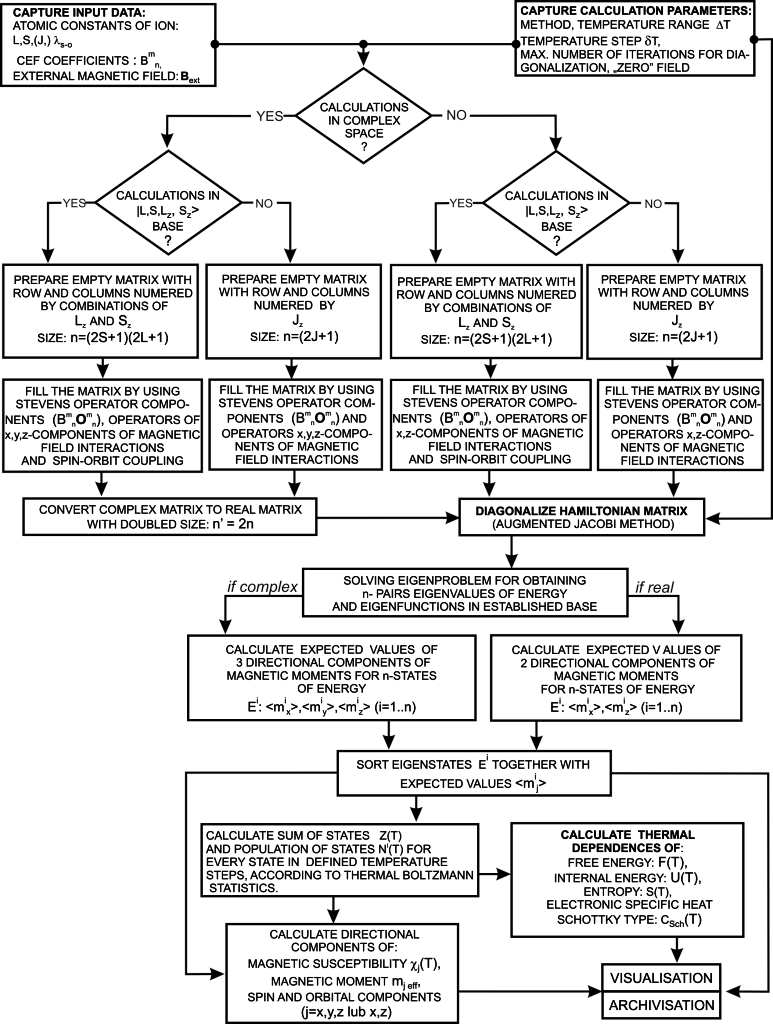
The diagram below shows one cycle of the ATOMIC MATTERS calculation algorithm:
WHAT PROPERTIES OF MATERIALS CAN WE PREDICT?
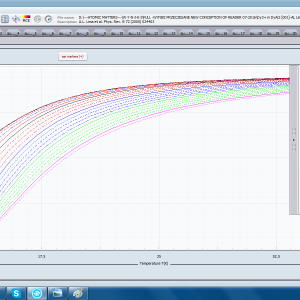
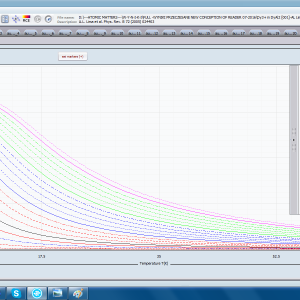
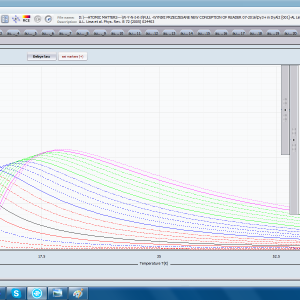
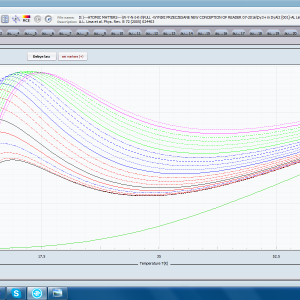
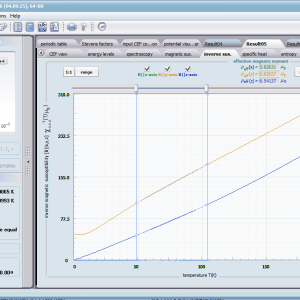
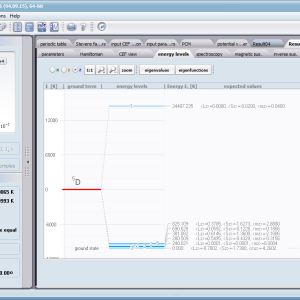
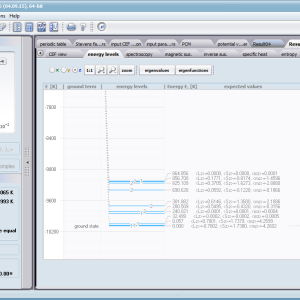
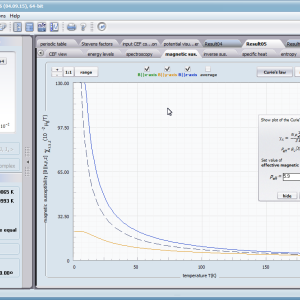
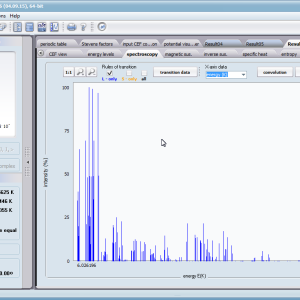
ATOMIC MATTERS allows you to simulate the single-ion properties of a crystal, strictly calculated on the basis of the properties of localized electron systems, with full control of parameters and computational methods. Consequently, ATOMIC MATTERS makes it possible to quantify the macroscopic properties of real, physically manufacturable or existing crystalline materials or to predict the properties of crystals currently not synthesized. The adopted methods and techniques of calculation and visualization make it possible to determine the full three-dimensional (3D) distribution of the magnetic properties (magnetic susceptibility, effective momentum, spin and orbital components, the expected values of magnetic moments in states and their components L,S,J), spectral properties (system of states, eigenfunctions, transfer matrix of transition probability, etc.), and calorimetric properties (Schottky specific heat and magnetic entropy). All the above properties are simulated in the form of temperature dependencies within the range defined by the user. Of course, information is also available about the properties at T = 0 [K], where only the lowest level of a state’s structure is filled. The total magnetic moment of the system at T = 0 [K] is equal to the momentum of the ground state. Occupying states at nonzero temperatures determines the atomic magnetic properties of ions, directly affecting the macroscopic magnetic properties of the compound.
On the basis of the structure of multi-electron states obtained as a consequence of the above calculations in the adopted basis (|L,S,J,Jz> or |L,Lz, S,Sz> with selection suggested for the type of ion), the following properties are predictable for all temperature dependencies obtained at a temperature range defined by the user, such as:
- Electron entropy – related to the temperature filling of multi-electron states of the calculated electron structure of an ion or atom Se (T)
- Electron component of specific heat - related to the temperature filling of multi-electron states of the calculated electron structure of an ion or atom. cSch(T)
- Magnetic moment and magnetization, and its directional components in a defined coordinate system; mi(B,T)
- Magnetic susceptibility and its directional components; χi(T)
- Spectroscopic observability of inter-state transitions; <Γi|J_|Γj>, <Γi|J+|Γj>, <Γi|JZ|Γj>
- Spin and orbital component of the total magnetic moment; <Γi|L|Γi>, <Γi|S|Γi>