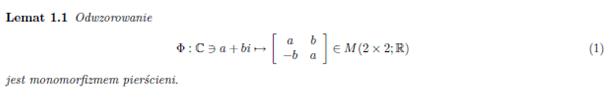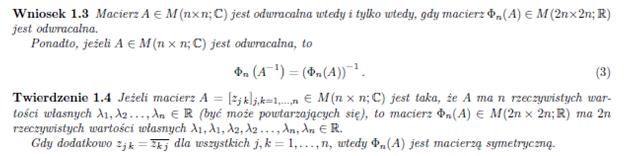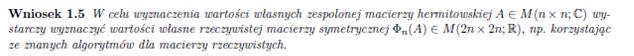MATRIX CALCULATIONS
Calculations of the magnetic properties of actual crystalline materials that contain metal ions with unclosed electron shells 2p, 3p, 3d, 4d, 5d, 4f and 5f require working with large matrices with complex field elements. The major matrix calculations are based on diagonalization of the complex Hamiltonian matrix of interactions using the Jacobi method, adapted to the requirements of ATOMIC MATTERS.
JACOBI DIAGONALIZATION
The Jacobi method is an iterative method intended to solve the full eigenproblem of real symmetric matrices. In the Jacobi method, the matrix A is converted by the similarity of a series of rotations. These are chosen in such a way as to allow the constructed matrices Ak (A1 = A) to tend to D = diag (λi).
In the classical variant of the method in its k-th step, we shall search for the largest (in terms of module) off-diagonal element of the matrix Ak = (aij). Let us assume that it is apq. Ak is then converted by the orthogonal similarity by rotation Tpq. The Tpq transformation matrix is different from the identity matrix only by elements tpp = tqq = cosθ and tpq = - tqp = sinθ. Rotation angle θ is defined in such a way as to zero the largest off-diagonal element, i.e. apq. Therefore, we shall construct another matrix:
It is symmetrical, and differs from Ak only by elements in columns and rows numbered p and q. The condition that the element Ak+1 with index (p, q) is zero gives the following relationship:
From this dependence, we can easily find the θ angle and make further transformations. The Jacobi method is linearly convergent at first. After a large number of steps, the convergence becomes approximately square.


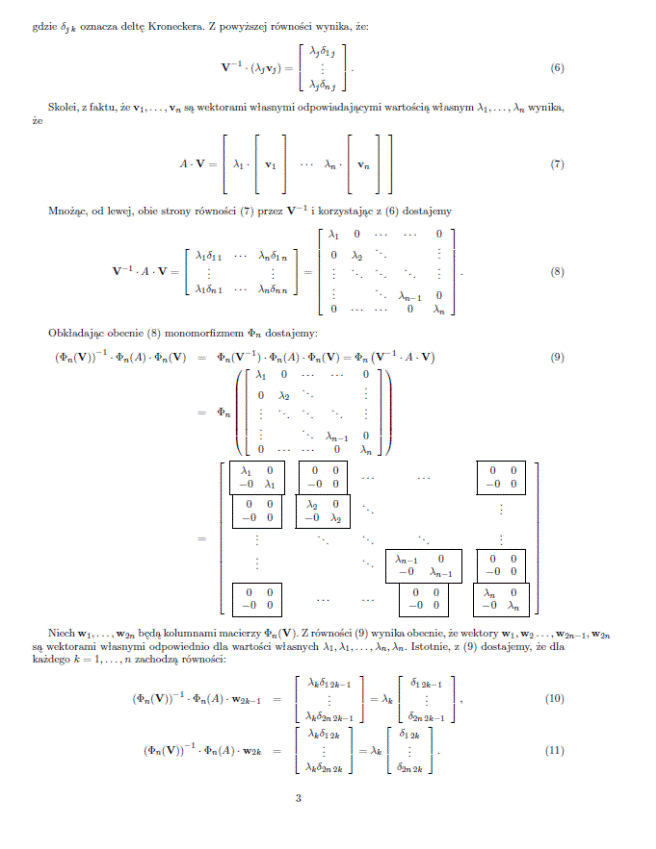
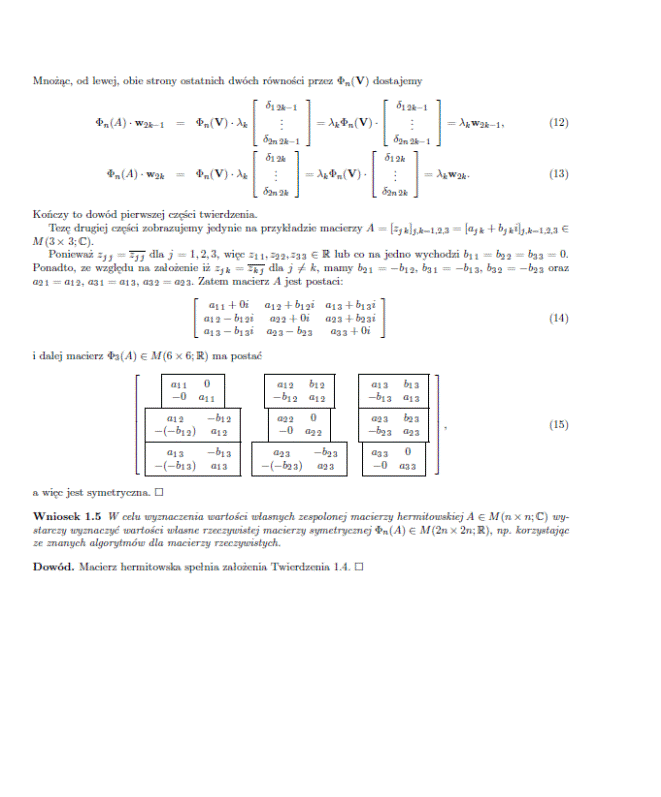
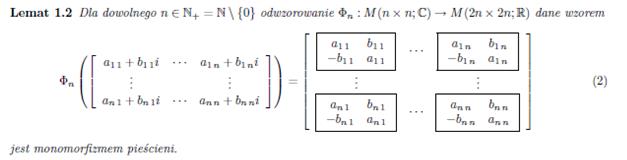
The exact matrix calculations, taking into account all three directions (x, y, z), require the use of complex matrices. A theory has been developed by Prof. dr hab. Marek Karaś that can convert and calculate such matrices and provides for expanding n x n dimensional matrices to 2n x 2n dimensional ones according to the following lemmas: