WSTĘP
Podejście teoretyczne, zastosowane w aplikacji ATOMIC MATTERS wywodzi się z technik i metod obliczeniowych fizyki atomowej i matematycznej teorii grup. Jądro zagadnienia stanowi teoria pola krystalicznego określana skrótem CEF (Crystal Electric Field), choć w literaturze przedmiotu można znaleźć inne akronimy (np. CF - Crystal Field, ZFS - Zero Field Splitting). Przyjęte podejście bazuje na metodach zdefiniowanych po raz pierwszy przez H.A. Bethe w 1929 roku ( Ann. Phys. Lpz. 3 (1929) 133 ). Teoria, której aspekty rozwijane były przez dekady przez najznakomitsze, często nagradzane najwyższymi naukowymi nagrodani, postacie nauki, wśród których należy wymienić: J.H. van Vleck, B.G. Wybourne, A.Abragam, B.Blaney, E.U. Condon, G.H. Shortley, R.J. Elliot, K.W.H. Stevens, M.T. Hutchings, G. Racah'a, B.R. Judd'a, P.G. de Gennes, J.Mulak, R.J.Radwański, C. Rudowicz, D.J.Newman i wielu innych, obecnie została zaimplementowana do aplikacji ATOMIC MATTERS.
Główne założenia teoretyczne podejścia stosowanego w ATOMIC MATTERS można streścić w kilku najważniejszych punktach:
- W jonach metali 2p/3p/3d/4d/5d/4f/5f istnieje struktura dyskretnych stanów elektronowych rzutujących na właściwości całego związku (kryształu).
- Układy wieloelektronowe 2pn, 3pn, 3d n, 4d n, 5d n, 4f n, 5f n stanowią silnie skorelowane systemy.
- Opis takich układów opiera się na fizyce atomowej, z liczbami atomowymi S, L, J całej powłoki. Skutkuje to przestrzenią n=(2S+1)(2L+1) stanów.
- W ciele stałym atom/jon oddziałuje ładunkowo z otoczeniem (efekt Starka) – to oddziaływanie prowadzi do znoszenia degeneracji stanów i określa się mianem Pola Krystalicznego CEF (Crystal Electric Field).
- Pole Krystaliczne, poprzez modyfikacje struktury subtelnej stanów elektronowych atomu determinuje właściwości atomu w ciele stałym i przekłada się na właściwości całego kryształu.
- Magnetyczne oddziaływania, zarówno wewnętrzne-między jonowe jak i z polem zewnętrznym prowadzą do dalszego znoszenia degeneracji stanów (efekt Zeemana).
- Sprzężenie spin-orbita wnosi istotny wkład w strukturę stanów i musi być uwzględnione w obliczeniach.
POLE KRYSTALICZNE (CEF)
Teoria pola krystalicznego CEF (Crystal Electric Field) została po raz pierwszy zaproponowana przez H.A. Bethe w 1929 roku. Przedstawione przez niego podejście wskazywało na możliwość przewidywania sposobu znoszenia degeneracji multipletów jonów paramagnetycznych. Podstawową ideą tej teorii było stwierdzenie, że pole elektryczne, wywierane przez koordynujące jony musi, zgodnie ze znanym wówczas od 16 lat zjawiskiem Starka, wpływać na stany elektronowe jonu paramagnetycznego, powodując ich rozszczepienie zależne od wartości krętowych liczb kwantowych. Oparte na teorii grup obliczenia wskazywały na możliwość ilościowego przewidywania sposobu rozszczepienia stanów elektronowych, w zależności od grupy punktowej symetrii otoczenia sieciowego jonu magnetycznego. U podstaw teorii pola krystalicznego (CEF – Crystal Electric Field) leżą tezy:
- siły odpowiedzialne za występowanie wiązania koordynacyjnego i jego trwałość mają charakter elektrostatyczny
- ligandy niezależnie od ich realnej struktury traktuje się źródło ładunku elekrostatycznego. Przestrzenny układ tych ładunków wyznacza symetrię pola elektrostatycznego działającego na jon centralny.
- konfiguracja elektronowa jonu centralnego jest określana na podstawie zasad kwantowo-mechanicznych, typowych dla fizyki atomu, ze strukturą subtelną termów i multipletów.
Rozwijana dalej przez m.in.: J.H.van Vleck'a, B.G. Wybourne'a, A.Abragam'a, B.Blaney'a, E.U. Condon'a, G.H. Shortley'a, R.J. Elliot'a, K.W.H. Stevens'a, G. Racah'a, B.R. Judd'a; teoria pola krystalicznego opiera się na „technice operatorów równoważnych” (operator equivalent techniques bazującej na Twierdzeniu Wignera-Eckarta ), która w stosunkowo prosty sposób pozwala na ilościowe określenie wartości rozszczepienia stanów o tej samej wartości liczby całkowitego momentu pędu J niezamkniętej powłoki elektronowej w polu krystalicznym. Podstawowa idea techniki operatorów równoważnych polega na rozwinięciu potencjału elektrostatycznego ligandów na szereg multipolowy. Następnie poszukuje się takich operatorów krętowych będących kombinacjami J+, J_ i Jz, które spełniają te same związki transformacyjne co odpowiednie składowe rozwinięcia potencjału w szereg multipolowy (warunkiem jest by J było dobrą liczbą kwantową). W sytuacji gdy J nie jest dobrą liczbą kwantową, tak jak ma to miejsce podczas obliczania wpływu pola krystalicznego CEF na konfiguracje d-elektronowe, budowanie operatorów równoważnych jest analogiczne i oparte o L+, L_ i Lz.
SUBTELNA STRUKTURA STANÓW WIELOELEKTRONOWYCH
Struktura dyskretnych poziomów atomowych niezamkniętych powłok 2p, 3p, 3d, 4d, 4f, 5f zawiera szereg stanów grupowanych w termy i multiplety. Wewnętrzny układ elektronowy w przypadku układu 3d stanowi rdzeń 18Ar . W przypadku układów 4f (5f) wewnętrzny rdzeń to 54Xe. Termy charakteryzują się tożsamością wartości liczb L i S i są formowane przez niecentralne, wewnątrzatomowe oddziaływania Coulombowskie. Stany termu zgrupowane w multiplety, charakteryzują się tą samą wartością L, S oraz J, i są formowane przez sprzężenie spinowo-orbitalne. Oddziaływanie spin-orbita jest zdecydowanie silniejsze w przypadku jonów ziem rzadkich i jonów aktynowców (4f, 5f) niż w przypadku jonów 3d w stosunku do oddziaływania CEF:
HCEF(3d ) > Hs-o(3d ); HCEF(4f,5f ) << Hs-o(4f,5f )
Zgodnie z tradycyjną klasyfikacją: silne sprzężenie spinowo-orbitalne powoduje, że J staje się względnie dobrą liczbą kwantową ponieważ pierwszy wzbudzony multiplet znajduje się przynajmniej ~130 meV (1500 K) powyżej multipletu podstawowego. Powoduje to, że jego obsadzenie w temperaturze pokojowej (300K) jest zaniedbywalnie małe. W takiej sytuacji, 2J+1 krotnie zdegenerowany multiplet podstawowy rozszczepiany przez zewnętrzne pole CEF może być traktowany jako podstawowy przyczynek do analizy właściwości takich układów. W przypadku obliczeń przylliżonych, dla bazy |J,Jz> Dla określenia który multiplet jest podstawowy stosuje się, znane z fizyki atomowej, reguły Hunda:
· Stan podstawowy struktury termów ma maksymalną wartość S, jaka tylko jest dozwolona przez zakaz Pauliego.
· Stan podstawowy posiada maksymalną dozwoloną wartość L, przy zachowaniu maksymalnego S.
· Podstawowemu multipletowi odpowiada J=|L-S|, gdy powłoka jest zapełniona mniej niż do połowy, a J=L+S, gdy zapełnienie jest większe.
Trzecia reguła Hunda stanowi podstawę dla prowadzenia obliczeń układów 4f oraz 5f-elektronowych w przestrzeni |J,Jz>.
Dla pełnych obliczeń, uwzględniających jednocześnie oddziaływania spinowo-orbitalne oraz CEF, zdodnie z klasycznym podejściem podręcznikowym, konieczne jest stosowanie metod perturbacyjnych lub obliczeń w bazie zawierającej całą strukturę multipletową podstawowego termu ataomowego |L,S,J,Jz> (a nie podstawowego multipletu jal w przypadku przestrzeni |J,Jz>). Zgodnie z klasycznym podziałem, taka sytuacja występuje w przypadku tzw. silnego pola krystalicznego jonów 3d (metale przejściowe grupy żelaza) poziomy struktury subtelnej grupują się w układy T2g, Eg, A2g, nie wykazując przynależności do konkretnych multipletów. W takiej sytuacji konieczne jest wzięcie pod uwagę całej struktury termów poprzez diagonalizację hamiltonianu o macierzy rzędu (2L+1)(2S+1). Tę metodologię można, oczywiście zastosować do obliczeń struktury stanów jonów 4f (lantanowców) i 5f (aktynowców) co w niektórych przypadkach pozwala uzyskać zaskakująco interesujące efekty. Niezmiennie jednak, w T = 0[K] (zero absolutne), tylko stan podstawowy struktury subtelnej jest obsadzony. Moment magnetyczny jonu/atomu jest równy wartości oczekiwanej momentu magnetycznego stanu podstawowego. Stany własne i odpowiadające im falowe funkcje wałasne hamiltonianu, |Γn>, uzyskuje się poprzez diagonalizacje Hamiltonianu CEF. Poziomy struktury subtelnejw zależności od użytej przestrzeni (reprezenatacji)|Γn>, wygladają następująco:
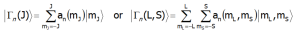
Metodologa zastosowana w aplikacji ATOMIC MATTERS pozwala zarówno prowadzić obliczenia w przestrzeni |J,Jz> podstawowego multipletu jak i w pełnej przestrzeni podstawowego termu LS: |L,S,Lz,Sz> dla każdego, dowolnie wybranego jonu/atomu występującego w przyrodzie. Co więcej, uporaliśmy się z zagadnieniami przeskalowania i parametryzacji współczynników pola CEF dla różnych konwencji, przestrzeni rachunkowych i układów jednostek. Interface w postaci hierarchicznej struktury zakładek pozwala na pełną interakcję z użytkownikiem posiadającym równoległą kontrolę wizualną nad obliczeniami, ich wynikami i jednocześnie dostępnymi narzędziami. Obliczenia właściwości w izostrukturalnych szeregach, weryfikacja danych literaturowych i eksperymentalnych, archiwizacja wyników w systemie ATOMIC MATTERS nigdy nie były tak proste i czytelne. Możliwość wykonywania błyskawicznych obliczeń macierzowych, ich wizualizacja i równoległa prezentacja wyników pozwala użytkownikowi w kilka sekund, samodzielnie oszacować użyteczność i efektywność poszczególnych sposobów obliczeń w wybranych przestrzeniach i konwencjach rachunkowych.
SPEKTROSKOPOWA OBSERWOWALNOŚĆ PRZEJŚĆ MIĘDZYSTANOWYCH
Subtelna struktura elektronowa jest obserwowana w szeregu metod spektroskopowych (ESR EPR, IR spectroscopy, Raman scattering itp.). Obecnie najlepsze metody badania subtelnej struktury elektronowej umożliwia spektroskopia nieelastycznego rozpraszania neutronów INS (Inelastic Neutron Scattering). Dla układu N identycznych jonów przyjmuje się różniczkowy przekrój czynny w eksperymentach INS jako:
![]()
W powyższym równaniu γN oznacza czynnik żyromagnetyczny neutronu, re jest klasycznym promieniem elektronu re=e2/(mec2)=2.818·10-15m, ki i kf oznaczają odpowiednio wektor falowy padającego i odbitego neutronu a wyrażenie exp(-2W(ki-kf)) reprezentuje czynnik Debye’a-Wallera opisujący termiczne wzbudzanie drgań atomów. Funkcja delta δ (ω - Ej + Ek) odpowiada nieskończenie wąskim stanom pola krystalicznego i często jest zastępowana w dokładnych obliczeniach rozkładem Lorentza z zadanymi szerokościami połówkowymi stanów CEF. Kwadrat elementów macierzowych z powyższego równania, symbolicznie oznaczany jako <Γk|J┴|Γj>2 w przypadku materiału polikrystalicznego dla dipolowych przejść zastępowany jest przez: ![]()
W przypadku monokryształu intensywność rozpraszania neutronów dla przejść dipolowych pomiędzy stanami CEF (Γj i Γk) przedstawia równanie:
![]() gdzie θ jest kątem pomiędzy wiązką neutronów a osią kwantyzacji z. INS jest bardzo silnym narzędziem pozwalającym na doświadczalną weryfikację teoretycznie obliczonej subtelnej struktury stanów elektronowych. Należy jednak pamiętać, że nie wszystkie stany CEF są widoczne tą techniką - widoczne są tylko te przejścia pomiędzy stanami, gdzie:|<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| nie jest zerowe. Obliczenia elektronowej struktury subtelnej prowadzone w dowolnej przestrzeni i konwencji dostępnej w systemie ATOMIC MATTERS dostarczją wartości elementów |<Γk|Jz|Γj>|, |<Γk|J-|Γj>| oraz |<Γk|J+|Γj >| lub analogicznych: |<Γk|Lz|Γj>|, |<Γk||<Γk|Sz|Γj>|, |<Γk|L-|Γj>|, |<Γk|L+|Γj >|, |<Γk|S+|Γj >| oraz |<Γk|S-|Γj>| dostarczając informacji bezpośrednio na diagramie stanów oraz wysyłając do wewnętrznego symulatora widm ATOMIC MATTERS.
gdzie θ jest kątem pomiędzy wiązką neutronów a osią kwantyzacji z. INS jest bardzo silnym narzędziem pozwalającym na doświadczalną weryfikację teoretycznie obliczonej subtelnej struktury stanów elektronowych. Należy jednak pamiętać, że nie wszystkie stany CEF są widoczne tą techniką - widoczne są tylko te przejścia pomiędzy stanami, gdzie:|<Γk|Jz|Γj>|, |<Γk|J-|Γj>|, |<Γk|J+|Γj >| nie jest zerowe. Obliczenia elektronowej struktury subtelnej prowadzone w dowolnej przestrzeni i konwencji dostępnej w systemie ATOMIC MATTERS dostarczją wartości elementów |<Γk|Jz|Γj>|, |<Γk|J-|Γj>| oraz |<Γk|J+|Γj >| lub analogicznych: |<Γk|Lz|Γj>|, |<Γk||<Γk|Sz|Γj>|, |<Γk|L-|Γj>|, |<Γk|L+|Γj >|, |<Γk|S+|Γj >| oraz |<Γk|S-|Γj>| dostarczając informacji bezpośrednio na diagramie stanów oraz wysyłając do wewnętrznego symulatora widm ATOMIC MATTERS.
BIBLIOGRAFIA
- R.J. Radwanski, N.H. Kim-Ngan, F.E. Kayzel, J.J.M Franse, D. Gignoux, D. Schmitt, F.Y. Zhang, J. Phys.: Condens. Matter4 (1992)
- 8853.R.J. Radwański, Z. Ropka & R. Michalski in: Magnetism and Electronic Correlations in Local-Moment Systems: Rare Elements and Compounds, edited by M. Donath, P.A. Dowben & W. Nolting, World Scientific (1998) 445-453
- H. Margenau & G.M. Murphy, The matematics of Physics and Chemistry, Princeton, New Jersey (1956)
- J. Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 215 (1953) 437.
- J. Elliot, K.W.H. Stevens, Proc. Roy. Soc. A 218 (1953) 553.
- M.T. Hutchings, Solid State Phys.16 (New York 1964 ) 227.
- P. Fulde in: Handbook on the Physics and Chemistry Rare Earth, Vol. 2 North-Holland. Inc. (1979).
- C. Rudowicz, J. Phys. C: Solid State Phys. 20 (1987) 6033.
- K. Huang Podstawy fizyki statystycznej PWN 2006; Tłumaczenie: Magdalena Załuska-Kotur
- P.W. Atkins ChemiaPrzewodnik po chemii fizycznej PWN 1997

