TEORIA

TERMODYNAMIKA UKŁADÓW WIELOELEKTRONOWYCH
Prezentowane podejście niesie ogromny potencjał analityczny. Obli­czane stany i energie własne przedstawionego hamiltonianu umożliwiają przewidywanie szeregu właściwości elektronowych i magnetycznych związków. Struktura stanów uzyskiwana przez rozwiązanie równania własnego hamiltonianu pozwala obliczyć właściwości magne­tyczne związku w temperaturach ekstremalnie niskich, takie jak: wartość momentu magnetycznego w stanie uporządkowanym, jego kierunek oraz zachowanie się momentów magnetycznych po przyłożeniu zewnętrznego pola magnetycznego. Pozwala ona również na obliczenia zmian fizycznych właściwości układu przy zwiększaniu temperatury, gdy wartości (i ewentu­alnie kierunki) momentów magnetycznych zmieniają się, podobnie jak zmienia się rozszczepienie stanów struktury subtelnej w samouzgodnionym polu molekularnym. Prezentowane podejście umożliwia analizę mechani­zmu formowania momentów magnetycznych i powstawania porządku magnetycznego.
W temperaturze T = 0 K obsadzony jest wyłącznie stan podstawowy. W tej sytuacji moment magnetyczny jonu jest dokładnie równy momentowi stanu podstawowego. W skrajnie niskich temperaturach jest możliwe wzbudzanie układu np. poprzez magnetyczne oddziaływanie z niskoener­getycznymi neutronami (jest to wykorzystywane w Spektroskopii Nieelastycznego Rozpraszania Neutronów INS). Należy jednak mieć na uwa­dze, że obserwowane przejścia są wzbudzeniami ze stanu podstawowego.Gdy rośnie temperatura prawdopodobieństwo obsadzania wyższych stanów rośnie zgodnie ze statystyką Boltzmanna. Liczba jonów w stanie o energii E_i w układzie o temperaturze T, to: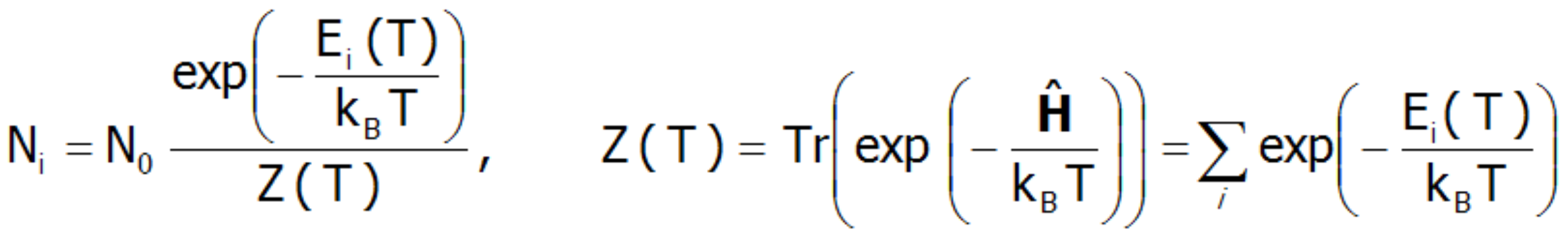

W powyższym wyrażeniu N oznacza całkowitą liczbę cząstek, a Z jest statystyczną sumą stanów (funkcją rozdziału). Znając statystyczną sumę stanów można określić energię swobodną Helmholtza F(T ):

Która pozwala oszacować energię wewnętrzną układu U(T ):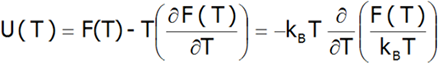

Na podstawie znajomości termodynamicznych funkcji stanu , można określić szereg właściwości układu zdefiniowanych w oparciu o nie. W szczególności termiczna oraz indukowana zewnętrznymi polami zmienność energii swobodnej F(T ) pozwala analizować termiczną ewolucję właściwości układów d lub f-elektronowych. Omówienie poszczególnych właściwości związków obliczanych w oparciu o przedstawioną metodę  w T ≠ 0 przedstawiono poniżej. Subtelna struktura stanów (E_i, Γ_i) pozwala na określenie termodynamicznych funkcji dla statystycznej grupy N jonów. Najrozsądniejszą wartością jest N=N_A≈6.022.10²³ mol^-1 (stała Avogadro).

ENTROPIA
Obliczanie entropii układu elektronów niezamkniętej powłoki d lub f sprowadza się do obliczenia całki:

gdzie c(T) oznacza obliczone ciepło molowe układu wzięte jako pochodna energii wewnętrznej po temperaturze:

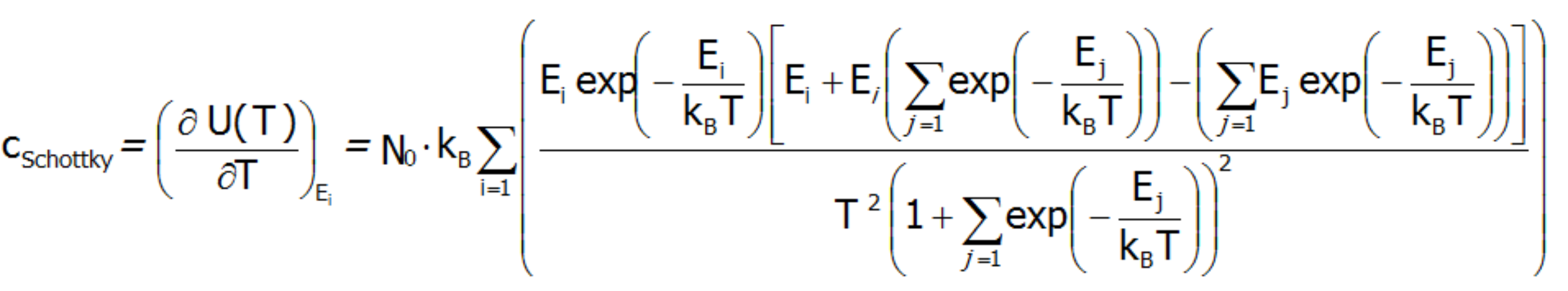
lub ciepło molowe obliczone wprost, jako druga pochodna energii swobodnej Helmoltza:

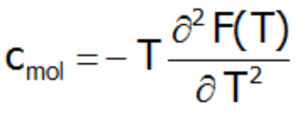 co w połączeniu z definicją entropii statystycznej pozwala na określenie ilości obsadzonych stanów subtelnej struktury elektronowej przy określonej temperaturze:

MOMENT MAGNETYCZNY I NAMAGNESOWANIE
Obliczanie namagnesowania, w przyjętej metodologii, sprowadza się do sumowania identycznie zachowujących się momentów magnetycznych poszczególnych jonów z niezamkniętą powłoką elektronową. Z uwagi na to, że jony ziem rzadkich znajdują się w samouzgodnionym polu molekularnym, wartość ich momentu magnetycznego zmienia się z temperaturą. Pamiętając, że z każdym stanem własnym hamiltonianu CEF związany jest jego moment magnetyczny, całkowity moment silnie skorelowanego układu elektronowego w danej temperaturze jest wypadkowym momentem z obsadzonych stanów obliczonym z wagą boltzmannowską: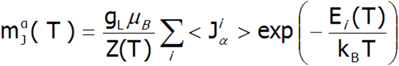

W powyższym równaniu indeks α – oznacza składową kierunkową, i – numeruje stany własne hamiltonianu, natomiast <Jⁱ_α > oznacza wartość oczekiwana rzutu całkowitego krętu całej powłoki na oś α  w i-tym stanie. Warto w tym miejscu podkreślić, że w T = 0 gdy obsadzony jest jedynie stan podstawowy, namagnesowanie układu jonów 4f w przeliczeniu na 1 jon jest równe wartości oczekiwanej momentu magnetycznego stanu podstawowego. Z uwagi na to, że w przyjętym modelu wszystkie jony zachowują się identycznie obliczona zależność temperaturowa momentu magnetycznego jest ściśle związana z wartością pola molekularnego, która wynosi:

Wartość współczynnika pola molekularnego n_mol określa temperaturę pojawiania się porządku magnetycznego T_c. Obliczenia namagnesowania w stanie uporządkowanym pozwalają wyznaczyć anizotropię magnetokrystaliczną układu. W przypadku symetrii tetragonalnej rozwinięcie energii anizotropii można przedstawić w znanej postaci:

gdzie K_i(T) są zależnymi od temperatury współczynnikami anizotropii, a θ i φ biegunowymi kątami opisującymi kierunek momentu magnetycznego względem wzajemnie prostopadłych osi krystalograficznych. Współczynniki K_i(T) są w ścisłym związku z parametrami pola krystalicznego. W polu o symetrii tetragonalnej mają one wartość [8]: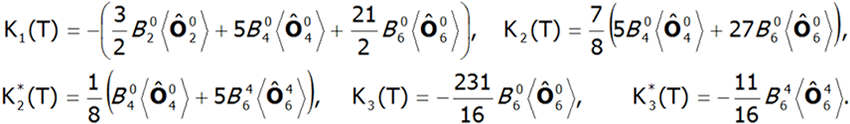

gdzie  oznacza średnie temperaturowe operatorów Stevensa. Możliwość obliczania wartości indukowanych momentów magnetycznych w polu zewnętrznym przyłożonym w różnych kierunkach pozwala na bezpośrednie określenie anizotropii magnetokrystalicznej.
Przedstawione podejście pozwala w klarowny sposób określić składowe całkowitego momentu magnetycznego jonów paramagnetycznych. Całkowity moment magnetyczny jonu składa się z części orbitalnej i spinowej: m_c=m_L+m_S. Znajomość wartości oczekiwanych składowych wektora momentu pędu poszczególnych stanów <Jiα > pozwala określić udział części spinowej i orbitalnej momentu magnetycznego. Pamiętając, że:

oraz biorąc pod uwagę, że g_l = 1 i g_s = 2.002324:

dostaje się:

Z powyższych związków wynika, że stosunki poszczególnych składowych momentu magnetycznego do momentu całkowitego są stałe dla danego jonu i niezależnie od otoczenia i temperatury:

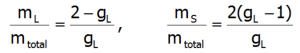
Zagadnienie dokładności powyższego rozumowania jest omówione na początku opisu podstaw teoretycznych aplikacji przy okazji porównania wyników obliczeń wykonywanych w bazie |J,J_z> w stosunku do obliczeń prowadzonych dla bazy pełniejszej |L,S,L_z,S_z > uwzględniających sprzężenie pomiędzy stanami różnych multipletów. Określenie wartości składowej orbitalnej i spinowej momentu magnetycznego jonu paramagnetycznego o strukturze elektronowej obliczanej w reprezentacji |L,L_z,S,S_z> sprowadza się do prostej interpretacji wartości oczekiwanych L i S. Zewnętrzne pole magnetyczne znosi degenerację, zmienia wartości energii stanów i miesza funkcje falowe stanów (efekt Zeemana). Znoszenie degeneracji i temperaturowo-zależne obsadzenie stanów prowadzi do formowania zależnego od temperatury momentu magnetycznego jonu. Namagnesowanie M obliczamy jako statystyczną sumę momentów poszczególnych jonów m.

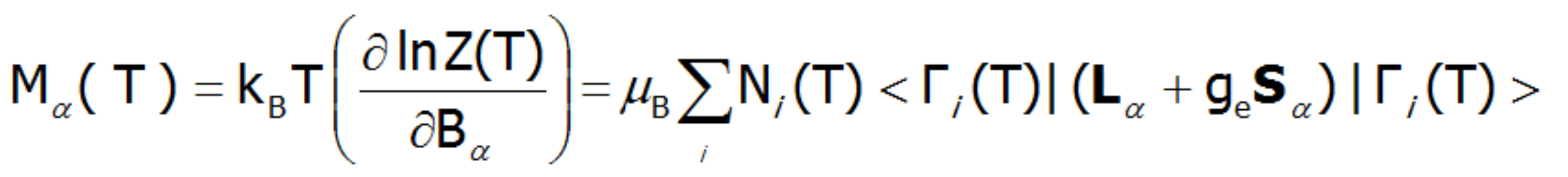
relacje jednostek :M[μ _B/ f.u.] ( 1μ _B = 9.27 ·10^-24 J/T,   J/T = A × m² )

gdzie:
α= x, y, z.
μ_B– Magneton Bohra,

g_L= czynnik Landego
k_B= 1,38 · 10 ^-23 J/K (stała Boltzmanna)

PODATNOŚĆ MAGNETYCZNA
Podatność magnetyczna dla stanu paramagnetycznego obliczana jest zgodnie ze swoją definicją jako stosunek indukowanego namagnesowania do przyłożonego pola magnetycznego. Biorąc pod uwagę związki pomiędzy funkcjami termodynamicznymi, w stosunkowo prosty sposób można obliczyć kierunkowe składowe temperaturowej zależności podatności magnetycznej silnie skorelowanego układu niezamkniętej powłoki elektronowej w strukturze krystalicznej. W granicy niskich pól zewnętrznych podatność definiuje się jako pochodną:

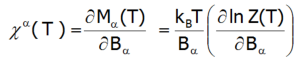
Gdzie index -α jest kierunkiem w lokalnym układzie współrzędnych związanym z osiami kwantyzacji powłoki w polu krystalicznym o określonej symetrii. Biorąc pod uwagę związki opisane w temacie TERMODYNAMIKA UKŁADÓW WIELOELEKTRONOWYCH, elementy macierzowe pomiędzy różnymi stanami otrzymuje się w granicy małych pól:

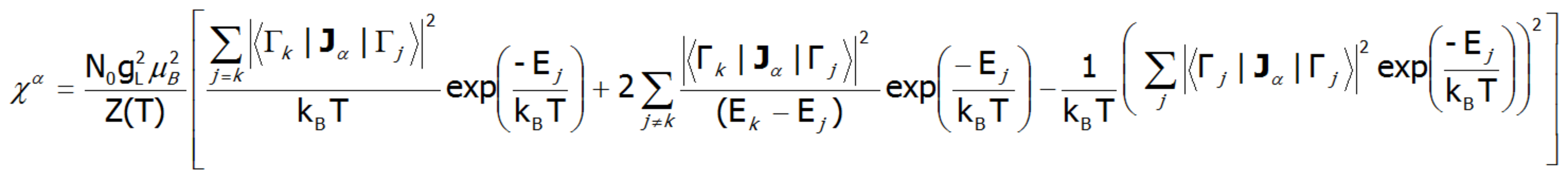
gdzie j, k numeruje stany własne hamiltonianu. Wyrażenie to dla wysokich temperatur, oraz dla bardzo słabych pól krystalicznych redukuje się do podatności typu prawa Curie. W temperaturach porównywalnych z wielkością rozszczepienia stanów pola krystalicznego krzywe podatności tej mogą znacząco odbiegać od kształtu hiperboli. W przypadku pól krystalicznych o niskiej symetrii podatność magnetyczna będzie wykazywać znaczną anizotropię. W strukturze kubicznej χ_x(T)= χ_y(T)= χ_z(T). Podatność magnetyczną można obliczać dla dowolnych pól zewnętrznych jako stosunek namagnesowania traktowanego jako suma indukowanych momentów magnetycznych, do przyłożonego pola. Z uwagi na często obserwowany nieliniowy wzrost wartości momentu magnetycznego, podatności obliczane dla różnych pól mogą się istotnie różnić.

SPEKTROSKOPOWA OBSERWOWALNOŚĆ PRZEJŚĆ MIĘDZYSTANOWYCH
Subtelna struktura elektronowa jest obserwowana w szeregu metod spektroskopowych (ESR EPR, IR spectroscopy, Raman scattering itp.). Obecnie najlepsze metody badania subtelnej struktury elektronowej umożliwia spektroskopia nieelastycznego rozpraszania neutronów INS (Inelastic Neutron Scattering). Dla układu N identycznych jonów przyjmuje się różniczkowy przekrój czynny w eksperymentach INS jako: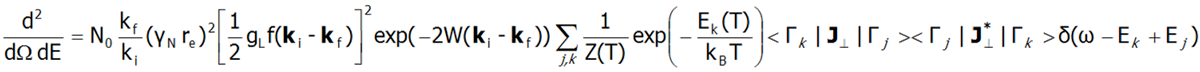

W powyższym równaniu γ_N oznacza czynnik żyromagnetyczny neutronu, r_e jest klasycznym promieniem elektronu r_e=e²/(m_ec²)=2.818·10^-15m, k_i i k_f oznaczają odpowiednio wektor falowy padającego i odbitego neutronu a wyrażenie exp(-2W(k_i-k_f)) reprezentuje czynnik Debye’a-Wallera opisujący termiczne wzbudzanie drgań atomów. Funkcja delta δ (ω - E_j + E_k) odpowiada nieskończenie wąskim stanom pola krystalicznego i często jest zastępowana w dokładnych obliczeniach rozkładem Lorentza z zadanymi szerokościami połówkowymi stanów CEF. Kwadrat elementów macierzowych z powyższego równania, symbolicznie oznaczany jako <Γ_k|J_┴|Γ_j>² w przypadku materiału polikrystalicznego dla dipolowych przejść zastępowany jest przez:

W przypadku monokryształu intensywność rozpraszania neutronów dla przejść dipolowych pomiędzy stanami CEF (Γ_j i Γ_k) przedstawia równanie: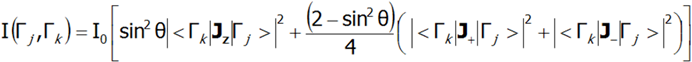

gdzie θ jest kątem pomiędzy wiązką neutronów a osią kwantyzacji z. INS jest bardzo silnym narzędziem pozwalającym na doświadczalną weryfikację teoretycznie obliczonej subtelnej struktury stanów elektronowych. Należy jednak pamiętać, że nie wszystkie stany CEF są widoczne tą techniką - widoczne są tylko te przejścia pomiędzy stanami, gdzie:|<Γ_k|J_z|Γ_j>|, |<Γ_k|J_-|Γ_j>|, |<Γ_k|J₊|Γ_j >| nie jest zerowe.

ELEKTRONOWE CIEPŁO WŁAŚCIWE TYPU SCHOTTKY’EGO
Ciepło właściwe typu Schottky’ego występuje wówczas, gdy mamy do czynienia z niskoenergetyczną strukturą dyskretnych stanów elektronowych. Aby określić czy w przypadku danego atomu będzie widoczna anomalia Shottyk’ego wystarczy znajomość struktury elektronowej tego pierwiastka, czyli sposobu w jaki elektrony zostały rozmieszczone na powłokach,  podpowłokach i orbitalach atomu. W szczególności istnienie subtelnej struktury elektronowej z blisko leżącymi poziomami energetycznymi zapewnia, że wkład c_sch będzie rozpoznawalny w obserwowanych zależnościach c_sch(T).

W sytuacji, gdy odległości pomiędzy poziomami struktury subtelnej nie zmieniają się, energia wewnętrzna układu dyskretnych stanów w T 0 obsadzonych boltzmannowsko, w przeli­czeniu na mol nieoddziałujących jonów paramagnetycznych, jest sumą energii całkowitych poszczególnych jonów. Gdy przy­jąć E₀ = 0 można ją przedstawić następująco: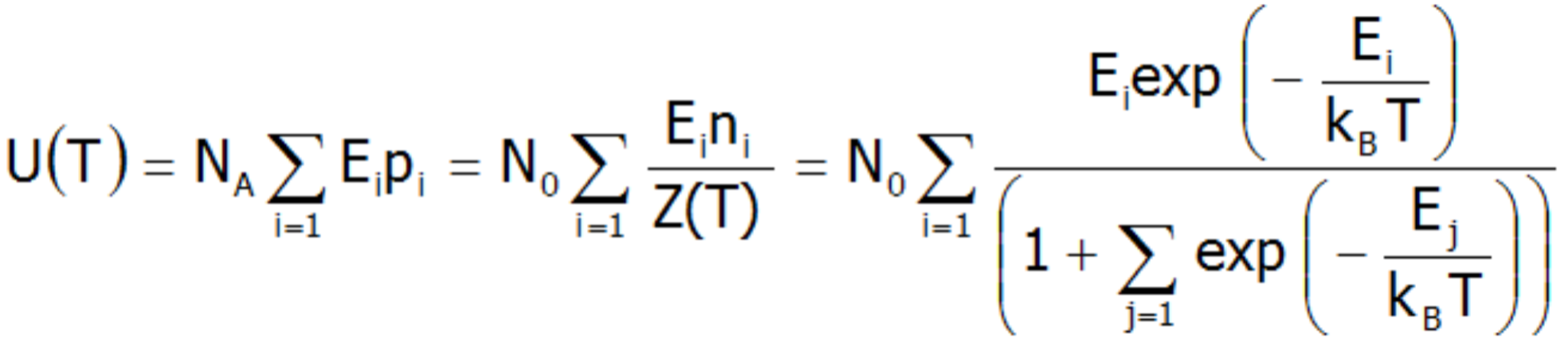

Zatem zgodnie z zasadami termodynamiki c(T) oblicza się pochodna energii wewnętrznej po temperaturze: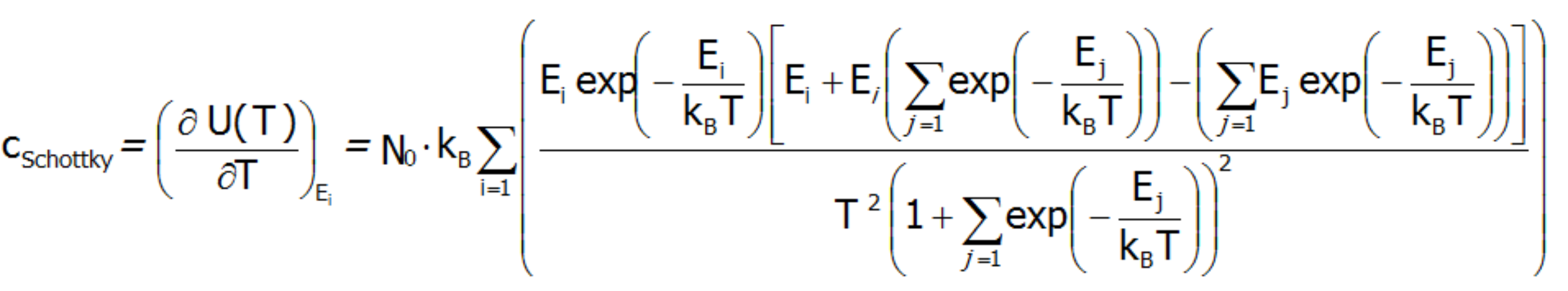

Krzywa anomalii Schottky’ego charakteryzuje się jednym lub kilkoma pikami. Często znając sam kształt tej krzywej jesteśmy w stanie na jej podstawie wyznaczyć układ poziomów energetycznych związku chemicznego. Wadą tej metody jest to, że możemy znaleźć kilka różnych układów poziomów energetycznych, które odpowiadają jednej krzywej. Aby wyznaczyć zależność ciepła Schottky’ego od temperatury wykonuje się dwa doświadczalne pomiary całkowitego ciepła właściwego. Mierzy się ciepło właściwe materiału z niezapełnioną powłoką 3d, 4d, 5d, 4f lub 5f a następnie dokonuje się pomiaru ciepła właściwego dla związku referencyjnego, którego jony mają powyższe powłoki zapełnione lub puste.

W przypadku gdy stany energii zmieniają się z temperaturą, tak jak się dzieje podczas procesu magnesowania powyższe obliczenia ciepła właściwego zastępuje się obliczeniami c(T) wprost z energii swobodnej Helmholtza F(T) poprzez numeryczne obliczenie jej drugiej pochodnej: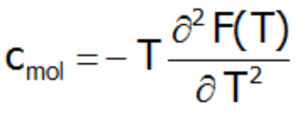

CIEPŁO SIECI KRYSTALICZNEJ
Aby przedstawić realistyczna postać całkowitego ciepła właściwego kryształu definiowanego poprzez jony paramagnetyczne i potencjał CEF do aplikacji wprowadziliśmy możliwość wizualizacji przebiegu zależności temperaturowej sumarycznego ciepła sieci krystalicznej w złożeniu z anomalią typu Schottky’ego. Symulowanie ciepła sieci wykonywane jest w oparciu o najbardziej znany i najszerzej akceptowany model definiowany w formalizmie opartym o fonony-kwantowane drgania cieplne sieci kryształu. Takie drgania można interpretować jako drgania własne oscylatorów harmonicznych i wyznaczyć ich energię [⁶]. Energia pojedynczego fononu to:

Fonon to kwant energii drgań sieci krystalicznej. Fonony mogą różnić się między sobą częstością, zatem aby obliczyć całkowitą energię sieci należy: wyznaczyć liczbę fononów o określonej częstości, wymnożyć ją przez energię fononu o tej częstości, a następnie zsumować energie otrzymane dla różnych częstości. Do wyznaczenia średniej ilości fononów o danej częstości używa się statystyki Bosego-Einsteina (tak zwanego rozkładu Bosego-Einsteina), danej wzorem: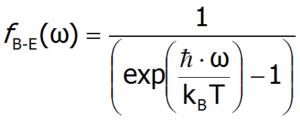

Wiedząc jakie częstotliwości mogą mieć fonony ciała stałego można wyznaczyć jego całkowitą energię sieciową, jednak dla uproszczenia, w rozważaniach dotyczących ciepła fononowego z dużym powodzeniem można korzystać z modelu Debey’a. Jeżeli długość łańcucha atomów składającego się z N atomów w sieci jednowymiarowej oznaczymy jako L, to możliwe długości fal obliczymy ze wzoru:

Ilość drgań w tej sieci wyznaczymy przekształcając powyższy wzór do postaci:

W trójwymiarowej przestrzeni ilość drgań o określonej częstości obliczamy analogicznie, jednak we wzorze pojawią się dodatkowe poprawki dotyczące stałych współczynników: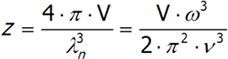

gdzie v jest prędkością dźwięku w próżni, V –to objętość kryształu, a ω częstotliwość. Ostatnie równanie różniczkujemy po ω. Pełną ilość drgań N atomów o trzech stopniach swobody, każdy obliczymy całkując powyższe wyrażenie otrzymujemy: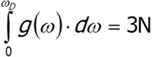

W modelu Debey’a nie wszystkie drgania są dozwolone, dlatego całkowanie wykonujemy od zera do ω_D czyli maksymalnej częstości drgań własnych, które mogą pojawić się w krysztale.

Obliczamy z ostatniego równania ω_D

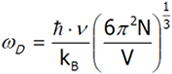
mnożymy obie strony równania przez

Otrzymane  równanie definiuje temperaturę Debey’a (Θ), czyli temperaturę przy jakiej w krysztale nie powstają już żadne nowe drgania normalne. Temperatura Debey’a określa również jak kryształ zachowuje się w danej temperaturze oraz w jaki sposób (w zależności od temperatury) należy liczyć dla niego ciepło właściwe.

Jeżeli temperatura kryształu jest niższa niż Θ, w krysztale rośnie amplituda drgań i powstają nowe drgania. W temperaturze wyższej od Θ, amplituda nadal rośnie, ale nowe drgania już nie powstają. Tabela 2.1 przedstawia wartości Temperatury Debey’a dla kilku pierwiastków. Żeby uzyskać wyrażenie na ciepło Debey’a należy najpierw obliczyć energie wewnętrzną, a następnie zróżniczkować ją po temperaturze. Dla uproszczenia obliczeń, przyjmujemy, że prędkość fononu nie zależy od jego polaryzacji. Przy takim założeniu, aby obliczyć całkowitą energię cieplną wystarczy obliczyć energię wewnętrzną dla jednej polaryzacji i pomnożyć ją przez trzy.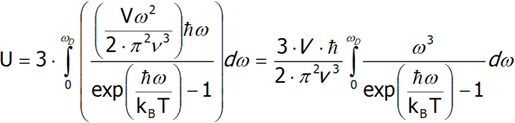

Różniczkując ostatnie równanie po temperaturze obliczamy pojemność cieplną.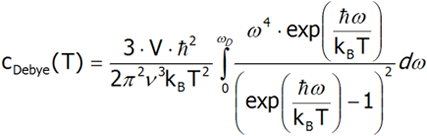

Powyższe równanie można uprościć dokonując zamiany zmiennych:

Ostatecznie, wyrażenie na ciepło Debey’a przyjmuje postać: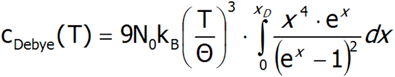

Taka postać wyrażenia na ciepło właściwe sieci krystaliczenej jest używana porównawczo w obliczeniach pojawiających się w pakiecie wynikowym w zakładce związanej z ciepłem właściwym, gdzie poprzez zdefiniowanie wartości Θ (w jednostakach: K) możemy obserwować sumaryczne ciepło sieci kryształu wraz z anomalią typu Schottky’ego (oczywiście jeśli występuje w zdefiniowanym przedziale temperatur).